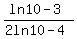SOLUTION: 10^(2x-1)=e^(4x-3)

You can put this solution on YOUR website!
10^(2x - 1) = e^(4x - 3)
ln(10^(2x - 1)) = ln(e^(4x - 3))
(2x - 1)ln(10) = 4x - 3
2x*ln(10) - ln(10) = 4x - 3
2x*ln(10) - 4x = ln(10) - 3
x(2*ln(10) - 4) = ln(10) - 3
x = (ln(10) - 3)/(2*ln(10) - 4)
About -1.1524

You can put this solution on YOUR website!

10^(2x-1)=e^(4x-3)

Apply ln function to both sides

ln 10^(2x-1)=ln e^(4x-3)

ln 10^(2x-1)=(4x-3)    --- After cancelling the ln and e on the right hand side.

(2x-1) ln 10 = (4x-3)

2xln 10 - ln 10 = 4x-3

2xln 10 - 4x = ln 10 - 3

x(2ln10 -4) = ln 10 -3

x =