Question 425890: Express as a single log
7^log base 7 45 + log base 6 3600
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!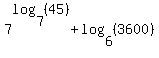 
Once you understand logarithms you will find the first term ridiculously easy to simplify.
Generally logarithms are exponents. 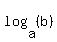 represents the exponent for "a" that results in "b". In other "words",  by definition of what a logarithm is!.
So  by definition. Now your expression is:
This is a single logarithm expression so it may be an acceptable answer. But the second logarithm can be simplified, too, because its argument, 3600, has a power of 6 factor:
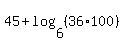
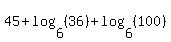
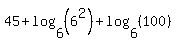
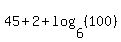
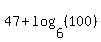
This is a simplified, single logarithm expression.
If the problem is literally to write the expression as just a single logarithm, then we need both terms to be in terms of base 6 logarithms. Since  and since multiplying by a 1 (no matter what form it is in) does not change a number we can rewrite the expression as:
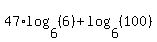
Now we can use a property of logarithms,  to move the coefficient of the first logarithm in the argumetn as its exponent:
Now we can use another property of logarithms, 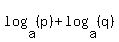 , to combine the two logarithms into one. (This property requires that the two logarithms have the same base (which is why we introduced the base 6 log to the first term) and coefficients of 1 (which is why we used the other property to move the 47 into the argument)) Using this property to combine the two logarithms we get:
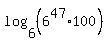
or
|
|
|
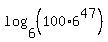
