Question 425232: Evaluate log2(log5 5).
I'm having trouble with logarithms in general, but evaluating in particular. Any help is greatly appreciated.
Found 2 solutions by lwsshak3, jsmallt9:
Answer by lwsshak3(11628)   (Show Source): (Show Source):
You can put this solution on YOUR website! Evaluate log2(log5 5).
..
The log of its base is always equal to 1. This answers the question: What number do I raise the base to equal itself. For example, for base 3, what number do I raise 3 to equal 3? You can see this will be 1 and it will hold for any base. Remember, the base raised to the logarithm of a number is equal to the number.
log5 5=1
log2(log5 5)=log2(1)
what do you raise the base 2 to get 1?
zero, as 2^0=1
ans:
log2(log5(5))=0
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
First some general things about logarithms. The idea behind logarithms is that it is possible to take any positive number (except 1) and, if you raise it to the right power, get any other positive number. The notation 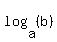 is read "Base a logarithm of b" but it represents the power of "a" that results in "b". is read "Base a logarithm of b" but it represents the power of "a" that results in "b".
Some of these "right powers" are well-known, some can be figured out with a good understanding of exponents and others pretty much require a calculator to figure out. Some examples: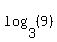 , the power of 3 that results in 9, is well known, , the power of 3 that results in 9, is well known,  so so  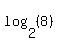 , the power of 2 that results in 8 is fairly well-known. , the power of 2 that results in 8 is fairly well-known.  so so   , the power of 12 that results in 1/12 is a little tricky. But if you understand negative exponents you'll realize that , the power of 12 that results in 1/12 is a little tricky. But if you understand negative exponents you'll realize that  so so  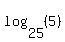 , the power of 25 that results in 5 is a little tricky, too. But with an understanding of fractional exponents we can figure out that, since an exponent of 1/2 means square root and since , the power of 25 that results in 5 is a little tricky, too. But with an understanding of fractional exponents we can figure out that, since an exponent of 1/2 means square root and since  , ,  . .
Some logarithms are nearly impossible to find without the use of a calculator. For example, 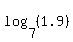 , the power of 7 that results in 1.9, is an exponent I can't imagine anyone could figure out without a calculator. (Note: Just because a logarithm like this is hard to find does not mean it doesn't exist. The idea behind logarithms says that any positive number (except 1), like 7, if raised to the right power, can result in 1.9 (or any other positive number)) So , the power of 7 that results in 1.9, is an exponent I can't imagine anyone could figure out without a calculator. (Note: Just because a logarithm like this is hard to find does not mean it doesn't exist. The idea behind logarithms says that any positive number (except 1), like 7, if raised to the right power, can result in 1.9 (or any other positive number)) So 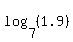 does exist. It just very hard to figure out. does exist. It just very hard to figure out.
Now let's finally look at your expression. As usual we start on the inside. So we'll look at just:
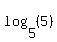
What power of 5 results in 5? This may be one of the easiest logarithms to find.  so so  . (In fact . (In fact  for all possible values of a (positive numbers except 1). Substituting this into your expression we now have: for all possible values of a (positive numbers except 1). Substituting this into your expression we now have:
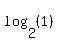
So what power of 2 results in a 1? With a good understanding of exponents we will know that any number (except zero) to the zero power is 1. (In fact,  for all possible values of a (positive numbers except 1)) for all possible values of a (positive numbers except 1))
So here's your problem from beginning to end:

|
|
|