Question 415427: 3 to the 2nd power x minus 1 = 3 to the third power
I hope I typed that problem in right, I don't know how to put it into the actual problem format. Anyway I don't understand how to solve these.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! You're right. You don't know how to post your problems. There are still five problems, all posted within a few minutes, which I suspect were all posted by you because of the similar way in which they were posted. I suspect that the reason that these problems have not received any responses from tutors is that they were unable to figure out what you were saying. For example, I have no clue what "3 to the 2nd power x minus 1" means. Is it
 or or
 or or
 or or
 or something else? or something else?
You will get more help with your questions if you can learn to express them in a way that others can understand. You can use English, mathematical notation or a mix of the two to describe your problems.
To use English you need to know how to read the problems correctly. What you posted might make sense to you but I doubt anyone else knows what it means. Ask your teacher, parents, friends, older brothers and sisters for help in learning how to read mathematical expressions correctly. Once you can read Math correctly you will probably understand it better and you will be better equipped to post questions.
To use mathematical notation you mostly just type what you see in the problem. However some expressions are difficult:- Exponents.
- Unless the base is just a number or a single variable, put the base in parentheses.
- Type a "^" character (shift+6) between the base and its exponent.
- Unless the exponent is just a number or single variable, put the ein parentheses.
- Fractions/division.
- Put parentheses around the entire numerator.
- Put a "/" character between the numerator and denominator
- Put parentheses around the entire denominator.
- Roots (square and other roots).
- Use "sqrt" to indicate a square root. Use something like "cuberoot", "4throot" to indicate other roots.
- Put the radicand in parentheses. (The expression inside a radcial is called the radicand.)
- Logarithms.
- Base 10 and base e (ln) logarithms are relatively easy to type. Logarithms of other bases are difficult to type because the base is written as a subscript. For these I suggest
- text like: "base 3 log of (x^2-4)"; or
- Learn and use Algebra.com's formula syntax. Probably the easies way to learn this is by clicking on "Show source". If you look on this web page right now, you will see "Show source" near the top of this response. If you click on it you will be able to see exactly what I typed. Look for three left braces. (A left brace is "{" and a right braces is "}".) Between the three left braces and the following three right braces is some of Algebra.com's formula syntax. By reading it and knowing how Algebra.com ends up displaying it, you can learn the syntax fairly quickly. By clicking on "Show source" now you will see how I was able to display the expressions at the beginning and these two additional examples:
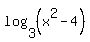 and and  . If you want to learn more about this syntax, I suggest that you poke around the various solved problems on Algebra.com and click on "Show source" on the ones you where you wonder: "How did they do that?" Click here to see the solution to a problem that may also help you to figure out the problems you posed. . If you want to learn more about this syntax, I suggest that you poke around the various solved problems on Algebra.com and click on "Show source" on the ones you where you wonder: "How did they do that?" Click here to see the solution to a problem that may also help you to figure out the problems you posed.
- Put the argument of the function in parentheses.
- If the base is more than just a number or single variable, put it in parentheses. For example: "base (x+2) log of (34)"
You might have noticed that parentheses are used a lot: bases of exponents and of logarithms, exponents, numerators, denominators, radicands and function arguments. Any expression that should be treated as a unit (like the above but not limited to the above) should be put in parentheses. When in doubt, use parentheses.
I hope this helps you become more successful with your posts on Algebra.com.
|
|
|