SOLUTION: PLEASE HELP solve for x: 9/2 log(base4)x=5

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: PLEASE HELP solve for x: 9/2 log(base4)x=5      Log On


   

Question 239148: PLEASE HELP
solve for x:
9/2 log(base4)x=5
Found 3 solutions by JimboP1977, jsmallt9, rapaljer:
Answer by JimboP1977(311) About Me  (Show Source):
You can put this solution on YOUR website!
(9/2)*log(base4) x = 5
log(base4)x = 5/(9/2)
log(base4)x = 5 * 2/9
log(base4)x = 10/9
x = 4^(10/9)
x = 4.666 to 3 decimal places.

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
%289%2F2%29%2Alog%284%2C+%28x%29%29+=+5
Solving logarithmic equations where the variable is in the argument of a logarithm is often done by transforming the equation into one of the following forms:
log(expression-with-variable) = other-expression
or
log(expression-with-variable) = log(other-expression)
The transformations can be done using basic Algebra and/or the properties of logarithms.

For your equation all we need to do to achieve one of these forms is to eliminate the 9/2. The easiest to to this is to multiply both sides of the equation by its reciprocal, 2/9:
%282%2F9%29%289%2F2%29%2Alog%284%2C+%28x%29%29+=+%282%2F9%295
which simplifies to
log%284%2C+%28x%29%29+=+10%2F9
which fits the first of the desired forms. To solve equations in this form we use the fact that log%28a%2C+%28p%29%29+=+q is equivalent to p+=+a%5Eq to rewrite the equation in exponential form:
x+=+4%5E%2810%2F9%29
Using a calculator on the right side we get:
x+=+4.6661161583044663
(Round this off as desired.)


Answer by rapaljer(4671) About Me  (Show Source):
You can put this solution on YOUR website!
%289%2F2%29+%2Alog%284%2Cx%29=5

First, multiply both sides of the equation by 2/9
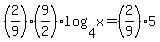
%282%2F9%29%2A%289%2F2%29+log%284%2Cx%29=%282%2F9%29%2A5
log%284%2Cx%29+=+10%2F9

Now, by the basic definition of logarithms:
log%28b%2Cx%29=y means b%5Ey=x

Likewise, log%284%2Cx%29+=+10%2F9 means that 4%5E%2810%2F9%29=+x

Is this okay for your final answer? You can also give the decimal approximation with a calculator. It comes out to approximately 4.666.

For additional help with this very important topic of Logarithms, I have quite a few resources--all FREE-- on my own website. To find my website, do a "Bing" search or a "Google" search for my last name "Rapalje". Near the top of the search list, look for "Rapalje Homepage." Near the top of my Homepage, look for the link "Basic, Intermediate, and College Algebra: One Step at a Time." Choose the link "College Algebra" and look in "Chapter 4" for topics on "Logarithms." In these sections, you will find my own non-traditional explanation especially designed for students that have trouble understanding their own books. My own explanations, together with examples and exercises, are also supported by my "MATH IN LIVING COLOR" pages in which I've solved the hardest problems IN COLOR.

I also have some videos of me teaching Logarithms in my own classes a few years ago. To see these videos FREE, go back to my Homepage and look for the link near the top of the page that says "Rapalje Videos in Living Color." Select "College Algebra", then look for "Logarithms Part I" and "Logarithms Part II."

In addition to these, I have a LOT of similar resources, both in written and video form, that may help you on a number of topics. Anyone can send me an Email at rapaljer@scc-fl.edu, and I'll be glad to tell you about the topics and pages that are available on the website.

Dr. Robert J. Rapalje, Retired
Seminole State College of Florida
Altamonte Springs Campus