Question 155464: How do i find the nth term for these sequences?
a) log [base 3], log [base 9] 81, log [base27] 81, log [base81]81
b) log[base 5]25, log [base 25]25, log [base 125]25, log [base 625]25
c) log [base m]m^k, log [base m^2]m^k, log [base m^3] m^k, log [base m^4]m^k
Is the nth term for c) log [base m^n]m^k? i'm not sure.
And also, the hard part about this question is that it said to write my expressions in the form p/q. How do I do this?
The exact question is : " Find an expression for the nth term of each sequence. Write your expressions in the form p/q where p, q are integers. Justify your answers using technology."
Thank you guys for your hard work!!
Answer by Earlsdon(6294)   (Show Source):
You can put this solution on YOUR website! Let's look at the first part, a:
a)  , , , ,...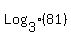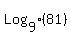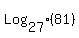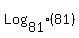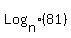
As you can see, the base (3 in this case) is raised to a power that is equal to the term number.
In the 1st term, the base, 3, is raised the the first power or 
In the second term, the base is raised to the second power or  and so on to the nth term, the power will be raised to the nth power or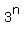 
Now you can work out the values of the first few terms by remembering the definition of a logarithm of a number.
"The logarithm of a number is the power to which the base of the logarithm must be raised to equal the number"
So, for the first term (n=1), we have:
 or...
 but we can express 81 as multiples of 3... , so we;ll substitute:
 therefore,  and so...
 for n = 1
Similarly for the second term (n=2), we have:
 and...
 or...
 and so...
 and  so we get:
 for n = 2
Let's look at the nth term:
 or
 so that:
 and
 so you can write:
 for the nth term. Where n is an integer =1, 2, 3, ...n
So if you apply the same logic to the rest of the problems, you should get the required answers.
Let's look at c)
As in the previous problems, the power of the base is equal to the number of the term, n.
 or...
 so that...
 and
 so...
If you are still having difficulties with these, please repost.
|
|
|
