SOLUTION: Given that 10^(2x)=0.2 and log5=0.6990, find value of x

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: Given that 10^(2x)=0.2 and log5=0.6990, find value of x       Log On


   

Question 1208655: Given that 10^(2x)=0.2 and log5=0.6990, find value of x
Answer by ikleyn(52778) About Me  (Show Source):
You can put this solution on YOUR website!
.
Given that 10^(2x)=0.2 and log5=0.6990, find value of x
~~~~~~~~~~~~~~~~~~ 

Notice that 0.2 = 1/5.  Therefore,  log(0.2) = 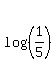log%28%281%2F5%29%29 = log(1) - log(5) = 0 - 0.6990 = -0.6990.

Now, we are given 

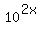    10%5E%282x%29 = 0.2.


Take logarithm base 10 of both sides.  You will get

      2x = log(0.2) = as we deduced above = -0.699.


Hence,  x = -0.6990/2 = -0.3495.    ANSWER


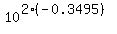CHECK.  10%5E%282%2A%28-0.3495%29%29 = 0.2000   (rounded),   which confirms the solution.

Solved.