Question 1205176: Prove by mathematical induction that 8𝑛 − 3𝑛
is divisible by 5 for all positive integers n
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
 is clearly a multiple of 5 when n is an integer.
Eg:
n = 1 leads to 5n = 5*1 = 5
n = 2 leads to 5n = 5*2 = 10
n = 3 leads to 5n = 5*3 = 15
--------------------------------------------------------------------------
If you meant to say  , then we can do a proof by induction.
Base case: n = 1
This proves that is a multiple of 5 when n = 1.
The base case is done.
Inductive Step:
Assume that  is a multiple of 5 for some integer k > 1.
That will mean  for some integer m.
Let's say we isolated the 8^k portion
which will be useful in a substitution step later.
The goal is to show that 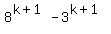 is also a multiple of 5 based on the assumption above.
This will produce a domino effect to prove is a multiple of 5 for any integer 
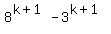
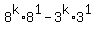
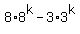
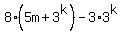 Substitution step. Replace 8^k with 5m+3^k.
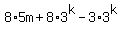
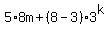
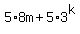
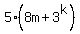
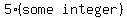
This proves that if is a multiple of 5, then 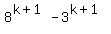is also a multiple of 5.
The inductive step is done.
This wraps up the induction proof.
More practice with induction proofs
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.1203186.html
--------------------------------------------------------------------------
Here's another approach to proving that is a multiple of 5 when n is an integer and
Let's look at the powers of 8
8^1 = 8
8^2 = 64
8^3 = 512
8^4 = 4096
8^5 = 32768
The units digits from top to bottom are: 8, 4, 2, 6, 8
Once we arrive at 8 again, the cycle repeats.
Therefore, those are the only units digits possible.
Note the cycle is 4 items long.
Let's look at the powers of 3
3^1 = 3
3^2 = 9
3^3 = 27
3^4 = 81
3^5 = 243
The units digits are 3, 9, 7, 1, 3
After arriving at 3 again, the cycle repeats.
Those are the only units digits possible.
Note the cycle is 4 items long, the exact same length as the previous cycle.
Let's arrange that info into a table.
| n | 8^n | 3^n | Units digit of 8^n | Units digit of 3^n |
|---|
| 1 | 8 | 3 | 8 | 3 | | 2 | 64 | 9 | 4 | 9 | | 3 | 512 | 27 | 2 | 7 | | 4 | 4096 | 81 | 6 | 1 | | 5 | 32768 | 243 | 8 | 3 |
When n = 1 the units digits for powers of 8 and 3 are 8 and 3 respectively.
8-3 = 5 shows is a multiple of 5 when n = 1.
When n = 2 the units digits for powers of 8 and 3 are 4 and 9 respectively.
Think of the 4 as 14 since we can borrow a ten.
Afterward 14-9 = 5 shows is a multiple of 5 when n = 2.
We don't have to look at the entire difference. All we need is the difference of the units digits.
Recall that a number is a multiple of 5 if it ends with 0 or 5.
When n = 3 the units digits for powers of 8 and 3 are 2 and 7 respectively.
Think of the 2 as 12 since we can borrow a ten.
Afterward 12-7 = 5 shows is a multiple of 5 when n = 3.
When n = 4 the units digits for powers of 8 and 3 are 6 and 1 respectively.
Subtract the units digits 6-1 = 5 to show is a multiple of 5 when n = 4.
For n = 5, it's a repeat of n = 1
n = 6 is a repeat of n = 2
n = 7 is a repeat of n = 3
and so on.
This concludes an alternate proof where we avoid induction.
Despite the fact this alternative is available, I recommend getting to know induction more because it shows up a lot in math proofs.
Also, it's a good idea to follow the teachers/textbooks instructions to get full marks.
Answer by ikleyn(52792)  (Show Source):
|
|
|
