Question 1171432: #1. Log2(3x-7)+log2(x+2)=log2(x+1)
#2. Log2(3x+1)-log2(2-4x)>log2(5x-2)
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Let's solve these equations step-by-step.
**Equation 1: Log₂(3x - 7) + Log₂(x + 2) = Log₂(x + 1)**
1. **Combine Logarithms:**
* Using the property Log(a) + Log(b) = Log(ab), we get:
* Log₂[(3x - 7)(x + 2)] = Log₂(x + 1)
2. **Remove Logarithms:**
* Since the logarithms have the same base, we can equate the arguments:
* (3x - 7)(x + 2) = x + 1
3. **Expand and Simplify:**
* 3x² + 6x - 7x - 14 = x + 1
* 3x² - x - 14 = x + 1
* 3x² - 2x - 15 = 0
4. **Solve the Quadratic Equation:**
* We can factor the quadratic equation:
* (3x + 5)(x - 3) = 0
* This gives us two possible solutions:
* 3x + 5 = 0 => x = -5/3
* x - 3 = 0 => x = 3
5. **Check for Valid Solutions:**
* We need to ensure that the arguments of the logarithms are positive.
* For x = -5/3:
* 3x - 7 = 3(-5/3) - 7 = -12 (Negative, invalid)
* x + 2 = -5/3 + 2 = 1/3 (Positive)
* x + 1 = -5/3 + 1 = -2/3 (Negative, invalid)
* For x = 3:
* 3x - 7 = 3(3) - 7 = 2 (Positive)
* x + 2 = 3 + 2 = 5 (Positive)
* x + 1 = 3 + 1 = 4 (Positive)
* Therefore, the only valid solution is x = 3.
**Solution for Equation 1: x = 3**
**Equation 2: Log₂(3x + 1) - Log₂(2 - 4x) > Log₂(5x - 2)**
1. **Combine Logarithms:**
* Using the property Log(a) - Log(b) = Log(a/b), we get:
* Log₂[(3x + 1) / (2 - 4x)] > Log₂(5x - 2)
2. **Remove Logarithms:**
* Since the logarithms have the same base, we can remove the logarithms:
* (3x + 1) / (2 - 4x) > 5x - 2
3. **Solve the Inequality:**
* First, we need to find the domain of the inequality:
* 3x + 1 > 0 => x > -1/3
* 2 - 4x > 0 => x < 1/2
* 5x - 2 > 0 => x > 2/5
* Combining these, the domain is 2/5 < x < 1/2.
* Now, let's solve the inequality:
* (3x + 1) > (5x - 2)(2 - 4x)
* 3x + 1 > 10x - 20x² - 4 + 8x
* 3x + 1 > 18x - 20x² - 4
* 20x² - 15x + 5 > 0
* 4x² - 3x + 1 > 0
* The discriminant of the quadratic is:
* (-3)² - 4(4)(1) = 9 - 16 = -7 (Negative)
* Since the discriminant is negative, the quadratic is always positive.
* Therefore, the inequality holds for all x in the domain 2/5 < x < 1/2.
**Solution for Equation 2: 2/5 < x < 1/2**
Answer by ikleyn(52776)  (Show Source):
You can put this solution on YOUR website! .
#1. Log2(3x-7)+log2(x+2)=log2(x+1)
#2. Log2(3x+1)-log2(2-4x)>log2(5x-2)
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution to equation #1 in the post by @CPhill, giving the answer x = 3,
is TOTALLY, GLOBALLY and FATALLY incorrect.
To check, it is enough to substitute x= 3 into equation #1.
You will get then in the left side
log_2_(3*3-7) + log_2_(3+2) = log_2_(2) + log_2_(5) = log_2_(2*5) = log_2_(10);
in the right side
log_2_(3+1) = log_2_(4),
and even by unarmed eyes, you see that the left side is not equal to the right side.
Contradiction which ruins the solution by @CPhill into dust.
Below is my correct solution.
Equation log_2_(3x-7) + log_2_(x+2) = log_2_(x+1) in its domain implies
(3x-7)*(x+2) = x+1
3x^2 - x - 14 = x+1
3x^2 - 2x - 15 = 0.
The discriminant is b^2 - 4ac = (-2)^2 - 4*3*(-15) = 4 + 180 = 184.
The discriminant is not a perfect square - so, the equation is not factorable.
Use the quadratic formula
 =  =  =  .
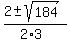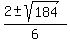The roots are  =  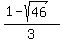= -1.92744,
and  =  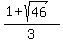= 2.59411 (approximately).
The root is not in the equation's domain - so, we reject it.
The root is in the domain, so we accept it, and this root is the unique solution to equation #1.
Equation #1 is solved.
You can check it on your own that my solution x = 2.59411 is correct, by substituting it into the equation.
I did it and obtained a perfect match.
|
|
|
