Question 1059175: What are the range and domain of F(x)=log6 x?
I know the x-intercept is (1,0) but I'm not sure how to use that information to find the answer. If you could show me the steps to find the answer in the future, i would really appreciate it.
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! F(x) = log6(x)
Yes, the graph of log6(x) passes through (1,0). The domain of x is the set of possible values x can take such that F(x) exists.
The "log" of a number is the exponent to which the base (in this case, 6) must be raised to give that number.
Does log6(x) exist for x<0? What about 0?
6^(0) = 1
6^(-1) = 1/6
6^(-2) = 1/36
6^(-100) = 1/6^100
etc.
Since 6 raised to any power is always >0 (yes we can get as close as we want to zero but never quite reach it), the domain of x is "all real numbers > 0" or we can say much more simply x>0.
The range applies to F(x). The range means "what values can F(x) take on over the domain of x?" (so domain applies to the input x to the function, range applies to the output F(x)). Since x can take on values greater than zero, we can make it arbitrarily close to zero, and hence F(x) becomes a larger negative number, without limit. Also, since x>0 is the domain, we can make x a large positive number without limit, hence F(x) can be as large as we want, without limit. So the range of F(x) is "all real numbers", sometimes we can write (-infinity, +infinity).
Domain: 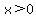
Range: 
—————————————————
Just to help solidify, here's another example:
Say we have y = sin(x)
x can be any value at all, but sin(x) only ranges from -1 to +1
So for y=sin(x), the domain is  and the range is and the range is 
|
|
|