Question 1043663: if log(a+b+c)=loga+logb+logc then prove that log(2a/1-a^2 + 2b/1-b^2 + 2c/1-c^2)= log 2a/1-a^2 + log 2b/1-b^2 + log 2c/1-c^2
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! We wish to show that  implies that implies that
 . .
For the result to have meaning, it must be that 0 < a,b,c < 1, which can be determined by solving the inequalities
 , ,  , and , and 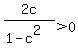 . .
With this in mind, it is enough to show that
a+b+c = abc ===>  . <---- Why? . <---- Why?
Now on to the proof:

===> , since a+b+c = abc, , since a+b+c = abc,
===> 
===> 
===> 
<===> 
<===>  after a little rearrangement of terms. after a little rearrangement of terms.
Since a+b+c = abc, we get

===> 
<===> 
<===> 
<===>  , after dividing both sides by , after dividing both sides by 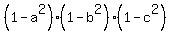
And that's it...
|
|
|