SOLUTION: Hi there. I am in grade 10 and I always have trouble with geometry. I have a question in my homework book that has been bothering me this weekend and I was wondering if you can hel

The vertices of a kite are A(4,8), B(7,4), C(10,5), and D(9,8). Verify that only ONE of the diagonals bisects the other diagonal

I am totally lost and I hope you could help me out as soon as possible.



First we have to find the point where the two diagonals AC and BD intersect.

To do that we find the equations of AC and BD.

We find the equation of AC:

Slope formula:
m = 
where (x1,y1) = A(4,8)
and where (x2,y2) = C(10,5)

m =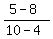 
m = 
m = 

Point-slope formula:
 y - y1 = m(x - x1)
where (x1,y1) = A(4,8)
 y - 8 = (x - 4)
 y - 8 = x + 2
     y = x + 10

Clear the fraction:

    2y = -x + 20
x + 2y = 20

---
We find the equation of BD:

Slope formula:
m = 
where (x1,y1) = B(7,4)
and where (x2,y2) = D(9,8)

m =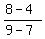 
m = 
m = 

Point-slope formula:
y - y1 = m(x - x1)
where (x1,y1) = B(7,4)
y - 4 = 2(x - 7)
y - 4 = 2x - 14
    y = 2x - 10

We solve the system of equations:



By substitution:

x+2(2x-10) = 20
   x+4x-20 = 20
     5x-20 = 20
        5x = 40
         x = 8
y = 2(8)-10 = 16-10 = 6

So the two (green) diagonals intersect at (8,6)

Now we show that (8,6) is the midpoint of BD

We use the midpoint formula:

Midpoint = 

where (x1,y1) = B(7,4)
and where (x2,y2) = D(9,8)

Midpoint = 
Midpoint = 
Midpoint = (8,6)

So we have proved that diagonal AC bisects diagonal BC.

Finally we have to show that BC does not bisect AC.

We show that (8,6) is NOT the midpoint of AC.

We use the midpoint formula again:

Midpoint = 

where (x1,y1) = A(4,8)
and where (x2,y2) = C(10,5)

Midpoint = 
Midpoint = 
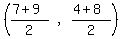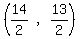Midpoint = (7,6.5)

So (8,6) is NOT the midpoint of AC.

Therefore, we have verified that only ONE of the diagonals, AC,
bisects the other diagonal, BD,

Edwin