Question 208991: How do you find the no. of terms in the following geometic sequence. 36+12+4+----+4/27. I know the formular but I seem to be getting the answer wrong.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! How do you find the no. of terms in the following geometic sequence.
36, 12, 4, ..., 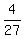 . I know the formula but I seem to be getting the answer wrong. . I know the formula but I seem to be getting the answer wrong.
To find the common ratio, r, we divide any term
by its preceding term.
So we can either divide the second term 12 by the
first term 36 and get  which reduces to which reduces to
 . So . So  or
we can divide the third term 4 by the second term 12
and get
or
we can divide the third term 4 by the second term 12
and get  which also reduces to which also reduces to  . So
either way we get . So
either way we get  .
I'll do it two ways, the first way we'll do it will not
be acceptable to your teacher, but it gets the right
answer, so you'll know when you get it right.
The first way is to write the terms out till you get
to .
I'll do it two ways, the first way we'll do it will not
be acceptable to your teacher, but it gets the right
answer, so you'll know when you get it right.
The first way is to write the terms out till you get
to 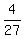 by multiplying by by multiplying by  each time:
36, 12, 4,
So to get the next term we multiply 4 by each time:
36, 12, 4,
So to get the next term we multiply 4 by  and get and get  .
So far we have:
36, 12, 4, .
So far we have:
36, 12, 4,  ,
To get the next term we multiply 4/3 by ,
To get the next term we multiply 4/3 by  and get and get  .
So far we have:
36, 12, 4, .
So far we have:
36, 12, 4,  , ,  To get the next term we multiply 4/9 by
To get the next term we multiply 4/9 by  and get and get 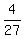 .
So that's it, we now have
36, 12, 4, .
So that's it, we now have
36, 12, 4,  , ,  , , 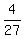 Then we count the terms and see that there are 6.
But your teacher doesn't want you to do that in case there
might have been 100 terms! But at least we know the answer
is 6.
Here's what your teacher wants to to do:
The formula for the nth term of a geometric sequence is
Then we count the terms and see that there are 6.
But your teacher doesn't want you to do that in case there
might have been 100 terms! But at least we know the answer
is 6.
Here's what your teacher wants to to do:
The formula for the nth term of a geometric sequence is



 Cross multiply:
Cross multiply:
 Simplify by dividing both sides by 4:
Simplify by dividing both sides by 4:
 Write
Write  and and  and and  as as 
 Add exponents on the right:
Add exponents on the right:
 Use the principle: If
Use the principle: If  and and 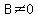 and and  then
then 

 Edwin
Edwin
|
|
|