SOLUTION: Hello.. I need to find the orthocenter of a triangle with coordinates: G(-2,5) H(6,5) J(4,-1) AND... A(4,-3) B(8,5) C(8,-8) Thanks to whoever answers this question!!!

Algebra ->  Formulas -> SOLUTION: Hello.. I need to find the orthocenter of a triangle with coordinates: G(-2,5) H(6,5) J(4,-1) AND... A(4,-3) B(8,5) C(8,-8) Thanks to whoever answers this question!!!      Log On


   

Question 174559This question is from textbook
: Hello..
I need to find the orthocenter of a triangle with coordinates:
G(-2,5)
H(6,5)
J(4,-1)
AND...
A(4,-3)
B(8,5)
C(8,-8)
Thanks to whoever answers this question!!! This question is from textbook

Answer by jojo14344(1513) About Me  (Show Source):
You can put this solution on YOUR website!

Let's draw the triangle with following vertices:
G(-2,5)
H(6,5)
J(4,-1)

Now, we draw a line from the vertex that is perpendicular to the opposite side.
1) from point G (-2,5) thru line HJ with points (6,5) & (4,-1):
m%5BHJ%5D=%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29=%28-1-5%29%2F%284-6%29=-6%2F-2
m%5BHJ%5D=3, Slope
Since perpendicular,m%5BG%5D=-1%2Fm%5BHJ%5D--->m%5BG%5D=-1%2F3
Then, via Slope-Intercept Form, y=mx%2Bb on point G:
5=%28-1%2F3%29%28-2%29%2Bb--->5=%282%2F3%29%2Bb
b=5-%282%2F3%29=%2815-2%29%2F3=13%2F3
Therefore, the line eqn ----->highlight%28y=%28-1%2F3%29x%2B%2813%2F3%29%29 , Line passing thru point G perpendicular to Line HJ
2) from point H (6,5) thru line GJ with points (-2,5) & (4,-1):
m%5BGJ%5D=%28-1-5%29%2F%284-%28-2%29%29=-6%2F%284%2B2%29=-6%2F6
m%5BGJ%5D=-1, Slope
Also, m%5BH%5D=-1%2Fm%5BGJ%5D---->m%5BH%5D=-1%2F-1=1
Then, via point (6,5):
5=1%286%29%2Bb---->b=5-6=-1
Therefore,
highlight%28y=1x-1%29, Line passing thru point H perpendicular to Line GJ
.
3)from point J (4,-1) thru Line GH with points (-2,5) & (6,5):
We can see Line GH has no Slope, only horizontal line (y=5), so line perpendicular to it from point (4,-1) is x%2B0%28y%29=4,highlight%28x=4%29 vertical line,slope is infinite
.
Plug in "highlighted" in the graph:
---------->
Graph on the LEFT, See LINES from one vertex perpendicular to the other side.
Graph on the RIGHT, Lines intersect at one point --->(4,3), orthocenter, ANSWER.
.
NEXT
Let's draw the Triangle with following vertices:
Points
A(4,-3)
B(8,5)
C(8,-8)

The same we did the last one,drawing a Line from the vertex that is perpendicular to the opposite side:
1)As you can see on point A (4,-3) is going thru vertical LINE BC and the line from point (4,-3) should be perpendicular to BC---->highlight%28y=-3%29
.
2)Point B (8,5) thru Line AC with points (4,-3) & (8,-8):
}
m%5BAC%5D=-5%2F4
And, m%5BB%5D=-1%2Fm%5BAC%5D, perpendicular right?
m%5BB%5D=-1%2F%28-5%2F4%29=4%2F5
Then,thru point (8,5): via Slope-Intercept Form y=mx%2Bb
5=%284%2F5%298%2Bb--->5=32%2F5%2Bb
b=5-%2832%2F5%29=%2825-32%29%2F5=-7%2F5
So, it follows ------->highlight%28y=%284%2F5%29x-%287%2F5%29%29
.
3)Point C (8,-8) thru line AB with points (4,-3) & (8,5):
m%5BAB%5D=%285-%28-3%29%29%2F%288-4%29=%285%2B3%29%2F4
m%5BAB%5D=8%2F4=2
Then, m%5BC%5D=-1%2Fm%5BAB%5D=-1%2F2
Thru point (8,-8):
-8=%28-1%2Fcross%282%291%29%2A%28cross%288%294%29%2Bb----->-8=-4%2Bb
b=-8%2B4=-4
It follows------>highlight%28y=%28-1%2F2%29%28x%29-4%29
.
Plug in "highlighted" in the graph;
------>
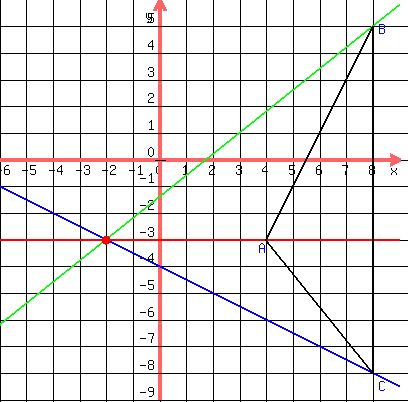
-------> Orthocenter lies outside the Triangle, being "Obtuse Triangle" >>>> point (-2,-3), ANSWER
Thank you,
Jojo