SOLUTION: Find coordinates for the centroid of the triangle whose vertices are (a) (-1,5), (-2,8) and (3,3); b) (2,7),(8,1) and (14,11); (c) (a,p), (b,q) and (c,r).

Algebra ->  Formulas -> SOLUTION: Find coordinates for the centroid of the triangle whose vertices are (a) (-1,5), (-2,8) and (3,3); b) (2,7),(8,1) and (14,11); (c) (a,p), (b,q) and (c,r).      Log On


   

Question 149703: Find coordinates for the centroid of the triangle whose vertices are (a) (-1,5), (-2,8) and (3,3); b) (2,7),(8,1) and (14,11); (c) (a,p), (b,q) and (c,r).
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!

The formula for the coordinates of the centroid is

x=%281%2F3%29%28x%5Ba%5D%2Bx%5Bb%5D%2Bx%5Bc%5D%29 and y=%281%2F3%29%28y%5Ba%5D%2By%5Bb%5D%2By%5Bc%5D%29

note: notice how we're simply averaging the coordinates

where , , and are the coordinates of the three vertices a, b, and c respectively.


a)

x=%281%2F3%29%28x%5Ba%5D%2Bx%5Bb%5D%2Bx%5Bc%5D%29 Start with the formula for finding the x-coordinate of the centroid.


x=%281%2F3%29%28-1-2%2B3%29 Plug in the x-coordinates of the given points


x=%281%2F3%29%280%29 Add


x=0 Multiply.


So the x-coordinate of the centroid is x=0

------

y=%281%2F3%29%28y%5Ba%5D%2By%5Bb%5D%2By%5Bc%5D%29 Start with the formula for finding the y-coordinate of the centroid.


y=%281%2F3%29%285%2B8%2B3%29 Plug in the x-coordinates of the given points


y=%281%2F3%29%2816%29 Add


y=5.33 Simplify.


So the y-coordinate of the centroid is y=5.33



So the centroid is (0,5.33)




b)



x=%281%2F3%29%28x%5Ba%5D%2Bx%5Bb%5D%2Bx%5Bc%5D%29 Start with the formula for finding the x-coordinate of the centroid.


x=%281%2F3%29%282%2B8%2B14%29 Plug in the x-coordinates of the given points


x=%281%2F3%29%2824%29 Add


x=8 Multiply.


So the x-coordinate of the centroid is x=8

------

(2,7),(8,1) and (14,11)
y=%281%2F3%29%28y%5Ba%5D%2By%5Bb%5D%2By%5Bc%5D%29 Start with the formula for finding the y-coordinate of the centroid.


y=%281%2F3%29%287%2B1%2B11%29 Plug in the x-coordinates of the given points


y=%281%2F3%29%2819%29 Add


y=6.33 Simplify.


So the y-coordinate of the centroid is y=6.33


So the centroid is (0,5.33)






c)

(a,p), (b,q) and (c,r).
x=%281%2F3%29%28x%5Ba%5D%2Bx%5Bb%5D%2Bx%5Bc%5D%29 Start with the formula for finding the x-coordinate of the centroid.


x=%281%2F3%29%28a%2Bb%2Bc%29 Plug in the x-coordinates of the given points



So the x-coordinate of the centroid is x=%281%2F3%29%28a%2Bb%2Bc%29

------

x=%281%2F3%29%28x%5Ba%5D%2Bx%5Bb%5D%2Bx%5Bc%5D%29 Start with the formula for finding the x-coordinate of the centroid.


x=%281%2F3%29%28p%2Bq%2Br%29 Plug in the x-coordinates of the given points


So the y-coordinate of the centroid is y=%281%2F3%29%28p%2Bq%2Br%29


So the centroid is (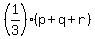%281%2F3%29%28a%2Bb%2Bc%29,%281%2F3%29%28p%2Bq%2Br%29)