Question 1207592: In triangle $ABC$, point $X$ is on side $BC$ such that $AX = 13,$ $BX = 13,$ $CX = 5,$ and the circumcircles of triangles $ABX$ and $ACX$ have the same radius. Find the area of triangle $ABC$.
Answer by ikleyn(53560)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In triangle ABC, point X is on side BC such that AX = 13, BX = 13, CX = 5,
and the circumcircles of triangles ABX and ACX have the same radius. Find the area of triangle ABC.
~~~~~~~~~~~~~~~~~~~~
I will solve the problem step by step.
Make a sketch and follow my reasoning.
Step 1. Triangle BAC is isosceles: angle C is congruent to angle B
Law of sine for triangle AXC, written for angle C, says
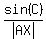 = = 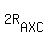 , (1)
where , (1)
where 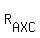 is the radius of the circle circumscribed about triangle AXC.
Law of sine for triangle AXB, written for angle B, says is the radius of the circle circumscribed about triangle AXC.
Law of sine for triangle AXB, written for angle B, says
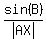 = = 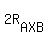 , (2)
where , (2)
where 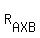 is the radius of the circle circumscribed about triangle AXB.
We are given that is the radius of the circle circumscribed about triangle AXB.
We are given that 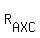 is equal to is equal to 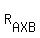 . Therefore, from (1) and (2) . Therefore, from (1) and (2)
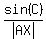 = = 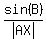 . (3)
It implies that sin(C) = sin(B). Since C and B are angles of triangle BAC, it implies
that angle C is congruent to angle B.
Thus, triangle ABC is isosceles, and side AC is congruent to side AB.
Step 1 is complete.
Step 2. Triangles BAC and AXB are similar
Indeed, both triangles ABC and AXB are isosceles and have common angle B, which is
the base angle for both triangles.
Thus step 2 is complete.
Step 3. Find the lateral sides AB and AC of triangle BAC
Let t be the common length of sides AB and AC of triangle BAC (now unknown).
In triangle BAC we know the length of its base BC = 13 + 5 = 18.
In triangle AXB we know the length of its lateral sides AX = 13 and BX = 13.
Since triangles BAC and AXB are similar, there is a proportion for ratios of corresponding sides . (3)
It implies that sin(C) = sin(B). Since C and B are angles of triangle BAC, it implies
that angle C is congruent to angle B.
Thus, triangle ABC is isosceles, and side AC is congruent to side AB.
Step 1 is complete.
Step 2. Triangles BAC and AXB are similar
Indeed, both triangles ABC and AXB are isosceles and have common angle B, which is
the base angle for both triangles.
Thus step 2 is complete.
Step 3. Find the lateral sides AB and AC of triangle BAC
Let t be the common length of sides AB and AC of triangle BAC (now unknown).
In triangle BAC we know the length of its base BC = 13 + 5 = 18.
In triangle AXB we know the length of its lateral sides AX = 13 and BX = 13.
Since triangles BAC and AXB are similar, there is a proportion for ratios of corresponding sides
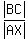 = = 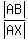 (it is base : lateral side = base : lateral side).
Substituting the values, this proportion takes the form (it is base : lateral side = base : lateral side).
Substituting the values, this proportion takes the form
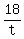 = = 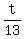 . (4)
From this proportion, t^2 = 18*13; hence, t = . (4)
From this proportion, t^2 = 18*13; hence, t = 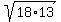 .
Thus, we found out the lateral sides of triangle BAC: |AB| = |AC| = .
Thus, we found out the lateral sides of triangle BAC: |AB| = |AC| = 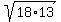 .
Step 3 is complete.
Step 4. Find the area of triangle BAC
For now, we know that triangle BAC is isosceles: AB= AC = .
Step 3 is complete.
Step 4. Find the area of triangle BAC
For now, we know that triangle BAC is isosceles: AB= AC = 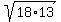 and its base BC has the length of 13+5 = 18 units.
Draw perpendicular AD (the altitude) from vertex A to the base BC.
It bisects the base BC in two parts of the length
and its base BC has the length of 13+5 = 18 units.
Draw perpendicular AD (the altitude) from vertex A to the base BC.
It bisects the base BC in two parts of the length 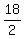 = 9 units.
The length h of the altitude AD will be (apply the Pythagoras)
h^2 = = 9 units.
The length h of the altitude AD will be (apply the Pythagoras)
h^2 = 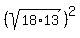 - -  = 18*13 - 81 = 153; h = = 18*13 - 81 = 153; h = 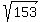 .
Now the area of triangle BAC is .
Now the area of triangle BAC is
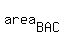 = = 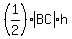 = = 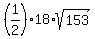 = = 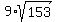 .
At this point, the problem is solved in full.
ANSWER. The area of triangle BAC is .
At this point, the problem is solved in full.
ANSWER. The area of triangle BAC is 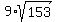 , or about 111.3238519 square units (approximately). , or about 111.3238519 square units (approximately).
Solved.
-------------------
Surely, this problem is of great Math Olympiad level.
|
|
|