SOLUTION: Find the general form of the equation of the plane passing through the points A (3, 2, 2), B (1,5, 0), and C (1, -3, 1). Use point A as 21, Y, 21 in the equation of the plane.

The solution is in two steps.


                   Step 1 - making equation of the plane parallel to the desired plane 
                            and passing through the origin of the coordinate system


Form vector AB_hat from point A to point B

     AB_hat = B-A = (1-3,5-2,0-2) = (-2,3,-2).


Form vector AC_hat from point A to point C

     AC_hat = C-A = (1-3,-3-2,1-2) = (-2,-5,-1).


Make 3x3-matrix

     M = .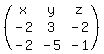


In this matrix, x, y and z are variables representing coordinates along x-, y- and z-axis;
the second row contains the components of vector AB_hat;
the third  row contains the components of vector AC_hat.


Write the determinant of matrix M, expanding the determinant by standard rules

    det (M) = x*(3*(-1)-(-5)*(-2)) - y*((-2)*(-1)-(-2)*(-2)) + z*((-2)*(-5)-(-2)*3) = -13x + 2y + 16z.


This equation 

       -13x + 2y + 16z = 0     (1)

determines the plane, parallel to the desired plane and passing  through the origin of the coordinate system.

                               Step 1 is complete.


                   Step 2 - making equation of the desired plane
                           

The desired plane has an equation of the form

       -13x + 2y + 16z = d.    (2)

Its left side is the same as in equation (1).


Right side "d" is a real value which we need to determine.
This value of "d" is the value of the linear function in the left side of equation (2),
calculated at any of the points A, or B, or C.


The interesting fact (actually, a key fact) is that the value of this function is THE SAME 
for all points A, B and C:


    for point A, it is  (-13)*3 + 2*2    + 16*2 = -3;

    for point B, it is  (-13)*1 + 2*5    + 16*0 = -3;

    for point C, it is  (-13)*1 + 2*(-3) + 16*1 = -3.


Thus finally, the desired equation is 

    -13x + 2y + 16z = -3.     ANSWER