Question 1201412: In a geometric series the seventh term is 1458, the ninth terms 13122. Find the second term algebraically
Found 3 solutions by Theo, ikleyn, math_tutor2020:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the formula for the geometric series is An = A1 * r ^ (n-1)
An is the nth term.
A1 is the first term
r ^ (n-1) is the common multiplier raised to the (n-1)th term.
in your problem, the seventh term would be A7 and the ninth term would be 9
you will have:
A7 = 1458
A9 = 13122
the formula for the 7th term is A7 = A1 * r ^ 6
the formula for the 9th term is A9 = A1 * r ^ 8
replace A7 and A9 with their respective values to get:
1458 = A1 * r ^ 6
13122 = A1 * r ^ 8
solve for A1 in both equations to get:
A1 = 1458 / r^6
A1 = 13122 / r^8
since they are both equal to A1, you get:
1458 / r^6 = 13122 / r^8
multiply both sides of the equation by r^8 and divide both sides of the eqution by 1458 to get:
r^8 / r^6 = 13122 / 1458
simplify to get:
r^2 = 9
solve for r to get:
r = 3
replace r in the first equation to get:
1458 = A1 * 3 ^ 6
solve for A1 to get:
A1 = 1458 / 3^6 = 2
replace A1 with 2 in the second equation to get:
confirm by replacing A1 in the first eqution to get:
1458 = 2 * 3 ^ 6 = 1458.
do the same in the secone equation to get:
13122 = 2 * 3 ^ 8 = 13122.
you have solved for A1 and r.
A1 is 2 and r is 3.
if you want to find the second term algebraically, you would get:
A2 = 2 * 3^1 = 6
that's your solution.
you could also have solved as follows:
A9 / A7 = (A1 * r^8)/A1 * r^6)
the A1 in the numerator and denominator cancel out and you are left with:
A9 / A7 = r^8 / r^6
simplify to get A9 / A7 = r^2
this becomes 13122 / 1458 = r^2
solve for r to get:
r = sqrt(13122 / 1458) = 3.
once you found r, then you can find A1 by just replacing r in the equation and solving for A1.
for example:
1458 = A1 * 3^6
this becomes 1458 = A1 * 749
solve for A1 to get:
A1 = 1458 / 729 = 2
you now have:
r = 3
A1 = 2
from there, you can easily find A2 because A2 = A1 * r ^ (2-1) which becomes A2 = 2 * 3 ^ 1 which becomes A2 = 2 * 3 which is equal to 6.
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a geometric series the seventh term is 1458, the ninth terms 13122. Find the second term algebraically
~~~~~~~~~~~~~~~~~~
Then  = = 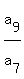 = = 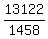 = 9.
Hence, either r= 3 or r= -3. "r" may have one of the two values.
As a consequence, = 9.
Hence, either r= 3 or r= -3. "r" may have one of the two values.
As a consequence,  may have one of the two values
If r= 3, then may have one of the two values
If r= 3, then  = =  = = 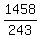 = 6,
or, if r= -3, then = 6,
or, if r= -3, then  = = 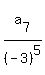 = = 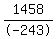 = -6.
Thus the problem has more than one solution/answer: it has TWO answers. = -6.
Thus the problem has more than one solution/answer: it has TWO answers.
Solved.
//////////////////
Be careful: @Theo produced long solution, but it is, factually, incorrect,
since one answer is LOST.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
r = common ratio, some nonzero value
a7 = 7th term = 1458
a8 = 8th term = a7*r = 1458r
a9 = 9th term = a8*r = (1458r)*r = 1458r^2
Each time we need a new term, we multiply the previous term by r.
Set the 9th term equal to the stated value 13122 and solve for r.
1458r^2 = 13122
r^2 = 13122/1458
r^2 = 9
r = sqrt(9) or r = -sqrt(9)
r = 3 or r = -3
We have two possibilities for r.
The negative r value will make the geometric sequence terms bounce around from positive to negative, or vice versa.
Consider the case r = 3.
an = a1*(r)^(n-1)
a7 = a1*(3)^(7-1)
1458 = a1*(3)^6
a1 = 1458/(3^6)
a1 = 2
One possible geometric sequence nth term formula is
an = 2*(3)^(n-1)
Check:
Plug in n = 7
an = 2*(3)^(n-1)
a7 = 2*(3)^(7-1)
a7 = 1458
Repeat for n = 9
an = 2*(3)^(n-1)
a9 = 2*(3)^(9-1)
a9 = 13122
Both values match up, so we've confirmed this formula is correct.
Now consider the case r = -3
an = a1*(r)^(n-1)
a7 = a1*(-3)^(7-1)
1458 = a1*(-3)^6
But hopefully you can see that (-3)^6 = 3^6 since the exponent is even.
Therefore, we'll land on the same starting a1 value we found earlier (a1 = 2).
We'll arrive at the formula an = 2*(-3)^(n-1)
I'll leave this check section to the student.
We have two possibilities for the nth term formula:
an = 2*(3)^(n-1)
an = 2*(-3)^(n-1)
Let's determine the 2nd term based on those formulas
an = 2*(3)^(n-1)
a2 = 2*(3)^(2-1)
a2 = 6
or
an = 2*(-3)^(n-1)
a2 = 2*(-3)^(2-1)
a2 = -6
------------------------------------
Conclusion:
The 2nd term is 6 if r = 3.
or
The 2nd term is -6 if r = -3.
|
|
|