Question 118694: The measure of an interior angle of a regular polygon is given. Find the number of sides in each polygon
1.) 120 2.)150
I am at a complete lost here, could someone help me please? Where would I start?
Found 2 solutions by scott8148, MathLover1:
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! the interior and exterior angles are supplementary (they add to 180°)
the sum of the exterior angles of a polygon is 360°
1.) 180-120=60 ___ 360/60=6 ___ hexagon
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Remember:
there are two methods to find the measure of the 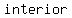 angles of a regular angles of a regular 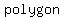 , and for both of them we will use the fact that the , and for both of them we will use the fact that the
 of the measures of the of the measures of the 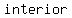 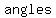 of a of a  is is  degrees degrees
  could be divided could be divided  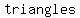
first method:
divide polygons into triangles by connecting one vertex to all of the others
you will see the 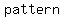 : :
if a polygon has  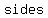 , we would be able to make , we would be able to make  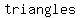
if a polygon has  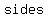 , we would be able to make , we would be able to make  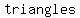
if a polygon has  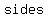 , we would be able to make , we would be able to make 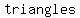
:
: and so on
if we have a polygon with  sides, we would be able to make sides, we would be able to make 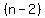 triangles triangles
So, in general, the measure of an interior angle of a regular 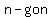 is: is:
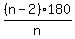
second method:
this method will be very similar to that of the first method;
the difference is that we will draw our triangles using one
point drawn  the polygon the polygon
let start with the square:
the square could be divided into  triangles; that means, the sum of all angles is triangles; that means, the sum of all angles is
 degrees degrees
however, we need to take off the sum of the angles around that middle point which is  degrees; degrees;
 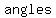 are are  involved with the involved with the 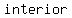 angles of the square angles of the square
so, we will have:
 degrees degrees
If we divide this sum of interior angles by the number of sides (or angles) in a square, we will get:
 degrees………..it is a measure of each interior angle in a square degrees………..it is a measure of each interior angle in a square
You can do same for other polygon.
In general, the measure of an 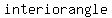 of a regular of a regular 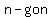 is: is:
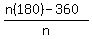
So, the number of sides in each polygon will be:
1.)
if the measure of 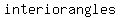 is is 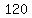 degrees, then the number of sides will be: degrees, then the number of sides will be:






 .............the number of sides .............the number of sides
2.)
if the measure of 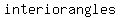 is is 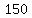 degrees, then the number of sides will be: degrees, then the number of sides will be:






 .................the number of sides .................the number of sides
|
|
|