Question 1165566: Generate the geometric sequence. Give the first 5 terms
A) First term is 7 and common ratio is 4
I got the answer 7,28,112,448,1792
B)First term is 10 and common ratio is -3
I got the answer 10,-30,90,-270,810
C)First term is 25 and third term is 900
I got the answer 25,150,900,5400,32400
D)First term is 8 and the fourth term is 1000
I got the answer 8,40,200,1000,5000
E)First term is -5 and the fifth term is -6480
I got the answer-5,-30,-180,-1080,-6480
I’m not quite sure about my answers 😅 did I do something wrong?
May I ask for your assistance in this two below I don’t quite get on how to get it’s terms because I’m not good at fractions
F)Fifth term is 3/256 and common ratio is 2
G)Sixth term is 7/4 and the seventh term is 1/2
Thank you for your assistance in advance 😁
Found 3 solutions by Theo, MathTherapy, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the formula for a geometric series is An = A1 * r ^ (n-1)
each succeeding term is multiplied by r
each preceding term is divided by 4.
A is correct.
B is correct.
C is correct.
D is correct.
E is correct.
so far you're did well.
F says the fifth term is 3/256 and the common ratio is 2.
the formula is An = A1 * r ^ (n-1)
replace A5 with 3/256 and r with 2 and n with 5 and the formula says 3/256 = A1 * 2 ^ 4 which becomes 3/256 = A1 * 16.
solve for A1 to get:
A1 = 3/256 / 16 which is the same as 3/256 * 1/16 which is equal to 3/4096.
A1 would be 3/4096.
A2 would be 2 * that = 6/4096.
A3 would be 2 * that = 12/4096.
A4 would be 2 * that = 24/4096.
A5 would be 2 * that = 48/4096.
that is your answer.
the only thing left to do, if they require it, is to simplify the fraction.
note that, for practical purposes, you do not have to simplify it since your calculator can easily handle these numbers.
in the first term, the denominator and the numerator are not divisible by any common integer, so it remains at 3/4096.
in the second term, the denominator and the numerator are divisible by 2.
divide both numerator and denominator by 2 and you get 3/2048.
in the third term, the denominator and the numerator are divisible by 4.
divide both numerator and denominator by 4 and you get 3/1024
in the fourth term, the denominator and the numerator are divisible by 8.
divide both numerator and denominator by 8 and you get 3/512.
in the fifth term, the denominator and the numerator are divisible by 16.
divide both numerator and denominator by 16 and you get 3/256.
your sequence, which was 3/1096, 6/4096, 12/4096, 24/4096, 48/4096, becomes:
3/4096, 3/2048, 3/1024, 3/512, 3/256.
G says the sixth term is 7/4 and the seventh term is 1/2.
the succeeding term is equal to r times the preceding term.
this means that 7/4 * r = 1/2.
multiply both sides of this equation by 4/7 to get:
r = 1/2 * 4/7 = 4/14 = 2/7.
the common ratio is 2/7.
to confirm, multiply 7/4 by 2/7 to get 14/28 = 1/2.
the common ratio of 2/7 is correct.
at this point in time, you shouldn't have to simplify fractions manually, especially monsters like the ones this problem gives you.
there are some calculators that can do that for you.
they can convert answers in decimal form to answers in simplified fraction form.
my calculator is the TI-84 Plus, which does both of these for me.
for example, i put 3764768 / 2151296 in the calculator and it tells me that the answer is 1.75 in decimal form.
to convert that answer to simplified fraction form, i do the following.
the answer in decimal form is in the calculator
i leave it there as is.
i press the MATH button.
i select 1:0>Frac
the calculator tells me the fraction is 7/4.
the number that i gave it was the fraction 3764768/2151296
the calculator gave me the answer in decimal form.
i then have the calculator convert that to simplified fraction form equal to 7/4.
this was the 6th term in the sequence.
the calculator told me that the sixth term is equal to 7/4 in simplified fraction form.
this confirmed for me that the ratio of 2/7 was correct.
if you got yourself a TI-84 Plus, you can do the same thing too.
they're about 100 dollars new, plus or minus, but you can get a used one on ebay for about 40, plus or minus.
in the absence of that, you can use an online fraction simplifier.
the one that i found is at http://www.alcula.com/calculators/math/simplify-fractions/
it seems to work quite well.
you give it the numerator and the denominator and it tells you the fraction in simplified form.
for example, i told it the numerator was 3764768 and the denominator was 2151296 and it told me that the simplified fraction was 7/4.
with a tool like this, you can keep your answer in unsimplified form and then have this tool simplify it for you.
you still need to know how to do fraction arithmetic, but the burden of simplifying the answer has been removed.
since you probably don't have the TI-84 Plus, i'll use the online calculator to simplify the fractions for you.
we determined above, that the common ratio is 2/7.
to find the preceding term, we have to divide by (2/7).
this is the same thing as multiplying by 7/2.
so, to find the preceding term, we have to multiply the current term by 7/2.
the common ratio is 2/7.
to find the next term, we multiply by 2/7.
to find the preceding term, we multiply by 7/2.
we'll work our way down to the first term.
sixth term is 7/4
fifth term is 7/4 * 7/2 = 49/8
fourth term is 49/8 * 7/2 = 343/16
third term is 343/16 * 7/2 = 2401/32
second term is 2401/32 = 16807/64
first term is 117649/128
the sequence, in unsimplified form, appears to be:
first term is 117649/128
second term is 16807/64
third term is 2401/32
fourth term is 343/16
fifth term is 49/8
sixth term is 7/4
i put these fractions into the fraction simplifier and it told me that they are all already in simplified form.
since none of these fractions can be simplified any further than they already are, then that's the answer.
with the online fraction simplifier, for example, i would enter 117649 as the numerator and 128 as the denominator and the calculator would tell me that the simplified fraction was 117649/128 which means that it was already in simplified form.
if i wanted to use the geometric sequence formula, i would have done the following.
i would have solved for r as i did before to get r = 2/7
the general formula is An = A1 * r ^ (n-1)
when n = 6, given the numbers that i have, the formula becomes:
7/4 = A1 * (2/7) ^ 5
(2/7) ^ 5 becomes 2^5 / 7^5 = 32/16807.
the formula becomes:
7/4 = A1 * 32/16807.
multiply both sides of this formula by 16807/32 to get:
7/4 * 16807/32 = A1
solve for A1 to get A1 = (7 * 16807) / (4 * 32) = 117649/128.
that's my first term.
each succeeding term will be multiplied by 2/7 until i get to the 6th term.
i take the sequence to the 6th term because that term is what i use to confirm my answer is correct.
without simplifying the fractions, i get:
first term = 117649/128
second term = 235298/896
third term = 470596/6272
four term = 941192/43904
fifth term = 1882384/307328
sixth term = 3764768/2151296
i use the fraction simplifier to determine that the sixth term is 7/4.
since this is what it's supposed to be, then the sequence is correct.
i then simplify all the fractions from the first term to the fifth term.
i get:
first term = 117649/128 = 117649/128
second term = 235298/896 = 16807/64
third term = 470596/6272 = 2401/32
four term = 941192/43904 = 343/16
fifth term = 1882384/307328 = 49/8
sixth term = 3764768/2151296 = 7/4
i previously got, by working backwards from the sixth term, the following sequence:
first term is 117649/128
second term is 16807/64
third term is 2401/32
fourth term is 343/16
fifth term is 49/8
sixth term is 7/4
the answer i got by using the formula is the same as the answer i got by working backward from the sixth term.
in this case, working backward from the sixth term was easier.
use of the ti-84 plus is much easier to convert your answer to simplified fraction form, but the fraction simplifier is also not very difficult to use.
again:
calculator i used is TI-84 Plus
online fraction simplifier i used is at http://www.alcula.com/calculators/math/simplify-fractions/
if you want more information on fraction arithmetic, here's a reference.
https://www.mathsisfun.com/algebra/fractions-algebra.html.
if you want to simplify fractions manually, here's a reference.
https://www.mathsisfun.com/simplifying-fractions.html
this reference also has a fraction simplifier that will simplify the fraction for you.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Generate the geometric sequence. Give the first 5 terms
A) First term is 7 and common ratio is 4
I got the answer 7,28,112,448,1792
B)First term is 10 and common ratio is -3
I got the answer 10,-30,90,-270,810
C)First term is 25 and third term is 900
I got the answer 25,150,900,5400,32400
D)First term is 8 and the fourth term is 1000
I got the answer 8,40,200,1000,5000
E)First term is -5 and the fifth term is -6480
I got the answer-5,-30,-180,-1080,-6480
I’m not quite sure about my answers 😅 did I do something wrong?
May I ask for your assistance in this two below I don’t quite get on how to get it’s terms because I’m not good at fractions
F)Fifth term is 3/256 and common ratio is 2
G)Sixth term is 7/4 and the seventh term is 1/2
Thank you for your assistance in advance 😁
Generate the geometric sequence. Give the first 5 terms
May I ask for your assistance in this two below I don’t quite get on how to get it’s terms because I’m not good at fractions
F)Fifth term is 3/256 and common ratio is 2
G)Sixth term is 7/4 and the seventh term is 1/2
In a geometric sequence, the preceding term is multiplied by the common ratio to get the following term. Therefore, to get the preceding term,
we DIVIDE a term by the common ratio to get the preceding term.
Applying this to F), we get: 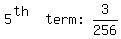

In a geometric sequence, a specific term is DIVIDED by its preceding term to get the common ratio of that geometric sequence.
Therefore, with  , we get: , we get: 
Now, we get: 
Answer by ikleyn(52788)   (Show Source): (Show Source):
|
|
|