SOLUTION: What is the value of cos(2α) , if 2 cos(3α)= cos(α)?

Algebra ->  Formulas -> SOLUTION: What is the value of cos(2α) , if 2 cos(3α)= cos(α)?      Log On


   

Question 1126751: What is the value of cos(2α) , if 2 cos(3α)= cos(α)?
Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.
Start from this basic identity


    cos(3a)=4*cos^3(a) - 3*cos(a).


Then 2*cos(3a) = 8*cos^3(a) - 6*cos(a),  and we are given that


    8*cos^3(a) - 6*cos(a) = cos(a).


It implies


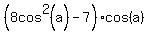    %288cos%5E2%28a%29+-+7%29%2Acos%28a%29 = 0.


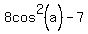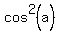So, either  cos(a) = 0   or   8cos%5E2%28a%29+-+7 = 0;  the last is equivalent to  cos%5E2%28a%29 = 7%2F8.


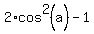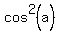Case 1.  If  cos(a) = 0,  then  cos(2a) = 2%2Acos%5E2%28a%29+-1 = -1.


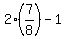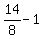Case 2.  If  cos%5E2%28a%29 = 7%2F8,  then  cos(2a) = 2%2Acos%5E2%28a%29+-+1 = 2%2A%287%2F8%29-1 = 14%2F8-1 = 6%2F8 = 3%2F4.


Answer.  If  2*cos(3a) = cos(a),  then EITHER  cos(2a) = -1  OR  cos(2a) = 3%2F4.

Solved.