SOLUTION: The segment from (-1,4) to (2,-2) is extended three times its own length. What is the terminal point

Draw a vertical line from (-1,4) down to (-1,-2), the point on a level 
with (2,-2).  Also draw a horizontal line from there over to (2,-2) to 
form a right triangle:



Notice that the vertical side of the right triangle is 6 units long and
the horizontal line is 3 units long.

Next extend the red vertical line from (-1,-2) to 3 times its length.  
It is already 6 units long so we need to extend it twice its length more
downward, so that it will be 18 units long.  So we must extend it 12 more 
units downward to make it 18 units long.  To do that will add -12 to its 
y-ccordinate, -2.  So we extend the vertical red line down to (-1,-14). 
Then from there we draw a horizontal line indefinitely long:



Next we extend the black line until it meets the lower horizontal 
red line:



We need to determine the coordinates for (?,?).  We already know that 
the y-coordinate is -14. We find the x-coordinate.  By similar triangles.
we first find the length of the horizontal side of the big triangle







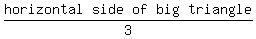
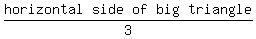Multiply both sides by 3.



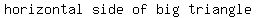So the point 9 units to the right of the point (-1,-14) is (8,-14)

Answer:  (8,-14)

Edwin