SOLUTION: Hi! I'm wondering how to solve for the orthocenter. Problem: Find the orthocenter of triangle JKL with vertices J(2,1), K(9,1), and L(4,6).

1.  Orthocenter is the common intersection point of altitudes of a triangle.

    (In any triangle, the three altitudes are concurrent and intersect in one point.)


    So all you need to do is to find the intersection of (any) two altitudes of the given triangle.


2.  One side of the triangle, the side JK, is horizontal line y = 1 in the coordinate plane, parallel to x-axis.
    Hence, the altitude to this side is a VERTICAL line parallel to y-axis. 
    Since this altitude passes through the point L=(4,6), the equation of this altitude is 
    
    x = 4.             (1)


3.  The side KL of the triangle has the slope m = 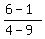 =  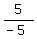= -1.

    Hence, the altitude of the triangle drawn to this side, has the slope 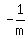 = 1 and, therefore,
    has an equation 

    y = x+b.           (2)


    Since this altitude passes through the point J(2,1), from the equation (2) we have 1 = 2 + b.
    Hence, b = 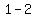 = -1 and finally, the equation (2) is

    y = x-1.           (3)


4.  Since we are looking for the intersection of the straight lines (1) and (3), we must solve these equations as a system.

    Then you have 

    y = 3.


Answer.  The orthocenter is the point  (x,y) = (4,3).