Question 1026674: Pls, help me with this question
A farmer has 120m of fencing with which to enclose a rectangular sheep-pen, using a wall for one side. Find the maximum area that he can enclose
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Question:
Pls, help me with this question
A farmer has 120m of fencing with which to enclose a rectangular sheep-pen, using a wall for one side. Find the maximum area that he can enclose
Solution:
This is a calculus question, but there does not seem to be a category for it.
The perimeter of the pen is 120=w+w+(120-2w), where w is the width and 120-w is the length opposite the wall.
The corresponding area is A(w)=w(120-2w)=120w-2w^2.
By completing squares,
A(w)=-2(w-30)^2+1800
We can see that when the first term vanishes, i.e. w=30, A(w) will be at its maximum.
So the maximum area is
A(30)=120*30-2*30^2=900, or w=30, L=120-2w=60.
Erratum:
The last line should read:
A(30)=120*30-2*30^2=3600-1800=1800, or w=30, L=120-2w=60, and area=1800 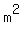
|
|
|