2 cars leave for a destination 48km away. Car B going at a speed
of 64km/hr started 12 minutes ahead of Car A which goes at a
speed of 100 km/hr. How long will it take Car A to overtake Car B?
Let t = the time it takes A to overtake B
Make this chart
DISTANCE | RATE | TIME
CAR A | |
CAR B | |
Fill in t for CAR A's time to overtake CAR B.
DISTANCE | RATE | TIME
CAR A | | t
CAR B | |
Fill in their given rates of speed:
DISTANCE | RATE | TIME
CAR A | 100 | t
CAR B | 64 |
Since CAR B had already been going 12 minutes,
CAR B's traveling time is 12 minutes longer than
CAR A's. 12 minutes is 12/60 hour or 1/5 hour.
So we add 1/5 hour to CAR A's x hours to get
CAR B's time. This is t + 1/5, so fill that in
for CAR A's time:
DISTANCE | RATE | TIME
CAR A | 100 | t
CAR B | 64 | t + 1/5
Now fill in the two distances by using DISTANCE = RATE(TIME)
DISTANCE | RATE | TIME
CAR A 100x | 100 | t
CAR B 64(t + 1/5) | 64 | t + 1/5
DISTANCE | RATE | TIME
CAR A 100x | 100 | t
CAR B 64(t + 1/5) | 64 | t + 1/5
They traveled the same distsnce to the point where CAR A
catches up, so we set the distances equal to each other:
100t = 64(t + 1/5)
100t = 64t + 64/5
Clear of fractions by multiplying through by 5
500t = 320t + 64
180t = 64
t = 64/180
t = 16/45 hr or (16/45)(60 minutes) =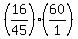 
t = 
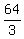minutes or 21 minutes 20 seconds.
Now the first piece of information
>>...2 cars leave for a destination 48km away...<<
was not used. However since it tells us they
are only going to travel for 48km, we must find
out whether car B had already gotten to the
destination before car A could catch up to it.
So we must calculate their distance to see.
It's 100x and 100(16/45 hr) = 35 5/9 km, so yes
car A did catch up to car B before it reached
its destination of 48 km.
Edwin
