Question 627564: how do i find the exterior angle of a convex polygon?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are two theorems that you can use to find the measure of interior angles of a convex polygon. One theorem works only for triangles. The other theorem works for all convex polygons, including triangles.
Let's take a look at the theorem for triangles first.
1. The sum of the interior angles of a triangle is always  ° °
Since the polygons can be divided into triangles, and since each triangle has 180°, you just multiply the number of triangles by  ° to get the sum of the ° to get the sum of the  angles. angles.

then divide it by  (number of the sides of a polygon) in order to calculate the measure of the (number of the sides of a polygon) in order to calculate the measure of the  angle angle

Use this theorem to find the measure of exterior angles of a convex polygon.
2. The sum of the exterior angles of a convex polygon is 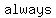  ° °
Remember that a straight angle is  ° °
The interior angle is always supplementary to an exterior angle at that vertex. They always add to  °, even for a concave polygon. °, even for a concave polygon.
Convex case:
In the case of convex polygons, where all the vertices point "outwards" away form the interior, the  angles are angles are 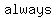 on the on the 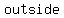 of the polygon. of the polygon.
Although there are  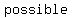 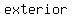 angles at each vertex , but we usually only consider one per vertex, selecting the ones that all go around in the same direction, clockwise in the figure. angles at each vertex , but we usually only consider one per vertex, selecting the ones that all go around in the same direction, clockwise in the figure.
Taken one per vertex in this manner, the exterior angles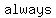 add to add to  ° °
This is true no matter how many sides the polygon has, and regardless of whether it is regular or irregular, convex or concave.
|
|
|