Question 59156: 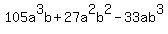 Can anyone help me solve this and more importantly, show me the process and some of the rules. Can anyone help me solve this and more importantly, show me the process and some of the rules.
Found 2 solutions by stanbon, fanks:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 105a^3b+27a^2b^2-33ab^3
1st: Find the largest common factor in the numbers:
It is 3
2nd: Find the largest common factor in powers of "a":
It is a
3rd Find the largest common factor in powers of "b":
It is b
4th:
Factor out the common factor:
It is 3ab
You get 3ab(35a^2+9ab-11b^2)
This is the most factoring you can do with
this algebraic expression. How do we know
that?
We can't find two numbers whose product is
35*-11=-385 and whose sum is 9
Chers,
Stan H.
Answer by fanks(6)   (Show Source): (Show Source):
You can put this solution on YOUR website! Does it equals zero? In that case...

From here (from the first multiplier) we can see that one solution is  , another is , another is  . .
What solutions are there from the second multiplier (from the second brackets)?
If 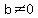 , we can divide both sides by , we can divide both sides by 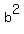 : :

Here we get a quadratic equation, let the quadratic equation solver solve this for us:
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=1621 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 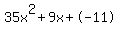 can be factored: can be factored:

Again, the answer is: 0.446594918262783, -0.70373777540564.
Here's your graph:
 |
So,  or or 
or
 or or 
Meaning that you can take very (infinitly) many different "a"s and "b"s as long as they have one of these two proportions.
So, along with the two zero cases (at the beginning), this is the solution of the given equation.
|
|
|