SOLUTION: Find the seventh term of (x^2-2)^9

Algebra ->  Expressions -> SOLUTION: Find the seventh term of (x^2-2)^9      Log On


   

Question 1163160: Find the seventh term of (x^2-2)^9
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52835) About Me  (Show Source):
You can put this solution on YOUR website!
.

The binomial expansion is this formula


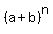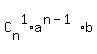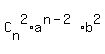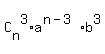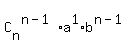    %28a%2Bb%29%5En = a%5En + C%5Bn%5D%5E1%2Aa%5E%28n-1%29%2Ab + C%5Bn%5D%5E2%2Aa%5E%28n-2%29%2Ab%5E2 + C%5Bn%5D%5E3%2Aa%5E%28n-3%29%2Ab%5E3 + . . . + C%5Bn%5D%5E%28n-1%29%2Aa%5E1%2Ab%5E%28n-1%29 + b%5En


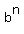In our case,  n = 9,  a = x^2,  y = -2.  Therefore, the general term of the binomial expansion in our case is  


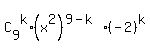    C%5B9%5D%5Ek%2A%28x%5E2%29%5E%289-k%29%2A%28-2%29%5Ek, k = 0, 1, 2, 3, 4, 5, . . . 


Then the 7-th term is at k = 6 


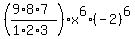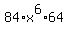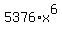    C%5B9%5D%5E6%2Ax%5E%2818-2%2A6%29%2A%28-2%29%5E6 = %28%289%2A8%2A7%29%2F%281%2A2%2A3%29%29%2Ax%5E6%2A%28-2%29%5E6 = 84%2Ax%5E6%2A64 = 5376%2Ax%5E6.    ANSWER

--------------

If you want to see other similar solved problems and to learn the subject wider and deeper,  then look into the lesson
    - Solved problems on binomial coefficients
in this site.

Also, you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this textbook under the topic
"Binomial expansion, binomial coefficients, Pascal's triangle".


Save the link to this textbook together with its description

Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson

into your archive and use when it is needed.


Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!
Find the seventh term of (x^2-2)^9
To find a SPECIFIC TERM of a binomial expansion, we use the formula: ,      

                                                                     where: 

We then get: 7th term of