|
Question 1084511: True or false: sin (x-180) = sin (180-x)
Could you explain this using the unit circle?
Sincerely,
Just a student trying to learn some maths
Found 2 solutions by Theo, MathTherapy:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! sine (180 - x) would give you the angle in the second quadrant, assuming the angle is originally in the first quadrant.
in other words, x is the angle in the first quadrant, therefore 180 - x is the equivalent angle in the second quadrant.
if x is in the first quadrant, then x - 180 would be the equivalent angle in the third quadrant.
sin(x) would be positive.
sin(180-x) would be also positive.
sin(x-180) would be negative.
this is because sine is positive in first and second quadrant and negative in second and third quadrant.
let's take an example:.
assume x = 30 degrees.
sin(30) = 1/2
180 - 30 would be equal to 150.
sin(150) = 1/2
sin(30) = sin(180 - 30)
30 - 180 would be - 150 degrees.
add 360 to it until it becomes positive and is between 0 and 360 degrees, and the equivalent angle is 210 degrees.
this angle is between 180 degrees and 270 degrees and is therefore in the third quadrant.
sin(210) = -1/2
the sine function is the same value except the sign of negative.
the following graph of the sine function and the value of y when x = 30 degrees, 150 degrees, and 210 degrees shows this to be true.
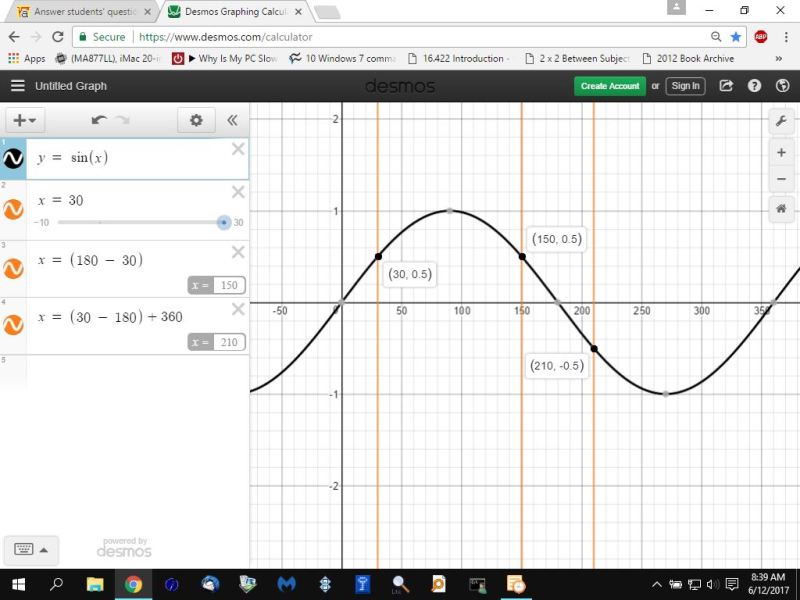
the following pictures show the different angle as seen on the unit circle.
30 degrees is in the first quadrant where the sign of the sine function is positive.
150 degrees is in the second quadrant where the sign of the sine function is still positive.
210 degrees is in the third quadrant where the sign of the sine function is negative.
note that 150 degrees is the equivalent angle of 180 - 30 degrees and is in the second quadrant.
note also that 210 degrees is the equivalent angle of 30 - 180 = -150 degrees which becomes 210 degrees after adding 360 to it in order to make it the positive equivalent of -150 degrees.
to answer your question:
your solution is that sin(180 - x) is not the same as sin(x - 180)
here's the unit circle pictures.
in the pictures, the format shown is (a,b) where a is the cosine of the angle shown and b is the sine of the angle shown.
you can see that (sqrt(3)/2,1/3) for 30 degrees means cosine 30 = sqrt(3)/2 and sine 30 = 1/2.
similarly cosine 150 degrees is - sqrt(3)/2 and sine 150 degrees is 1/2.
similarly cosine 210 degrees is -sqrt(3)/2 and sine 210 degrees is -1/2.

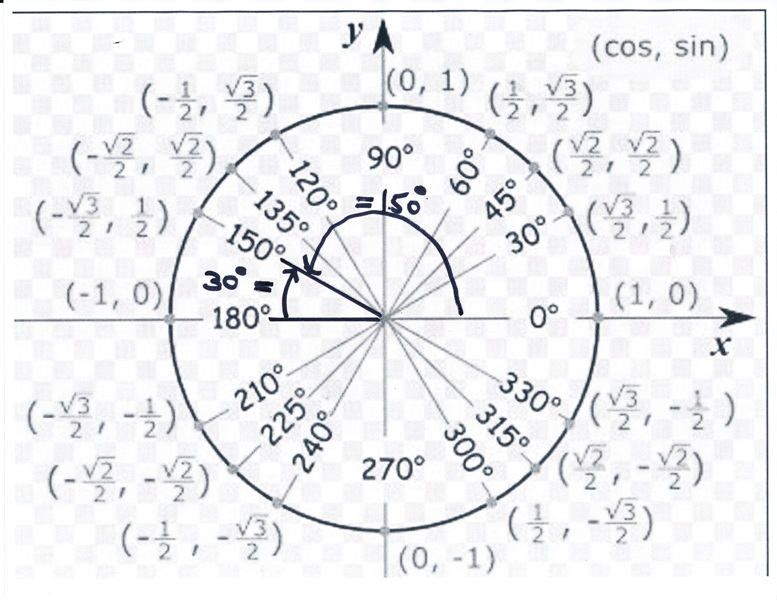

the sine function is positive in quadrants 1 and 2, and negative in quadrants 3 and 4.
the cosine function is positive in quadrants 1 and 4, and negative in quadrants 2 and 3.
some references you might find helpful.
https://www.mathsisfun.com/geometry/unit-circle.html
http://www.themathpage.com/atrig/unit-circle.htm
Answer by MathTherapy(10605)   (Show Source): (Show Source):
You can put this solution on YOUR website! True or false: sin (x-180) = sin (180-x)
Could you explain this using the unit circle?
Sincerely,
Just a student trying to learn some maths
The question is: "Is sin (x – 180) = sin (180 – x)?"
Look at the UNIT CIRCLE anywhere online and you'll see that cos 180 = - 1, and sin 180 = 0
sin (x – 180) = sin x cos 180 – cos x sin 180 --- Difference of angles' identity
sin (x – 180) = sin x * - 1 – cos x * 0 --------- Substituting – 1 for cos 180, and 0 for sin 180
sin (x – 180) = - sin x cos 180 – 0
sin (x – 180) = - sin x
sin (180 – x) = sin 180 cos x – cos 180 sin x --- Difference of angles' identity
sin (180 – x) = 0 * cos x – - 1 * sin x --------- Substituting 0 for sin 180, and – 1 for cos 180
sin (180 – x) = 0 + sin x
sin (180 – x) = sin x
Since:  . .
The assertion is therefore  . .
|
|
|
| |