Question 1043640: (a-2)x+(b+2)y=8
bx+ay=4
In the system of equations above a and b are constants. If the system has infinitely many solutions, what is the value of a ?
A) -4/3
B) -2/3
C) 2/3
D) 4/3
Answer by ikleyn(52824)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(a-2)x+(b+2)y=8
bx+ay=4
In the system of equations above a and b are constants. If the system has infinitely many solutions, what is the value of a ?
A) -4/3
B) -2/3
C) 2/3
D) 4/3
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(a-2)x + (b+2)y = 8, (1)
bx + ay = 4. (2)
In order for the system (1),(2) had infinitely many solutions,
this condition should be in place:
the ratio of coefficients at "x" is equal to the ratio of coefficients
at "y" AND equal to the ratio of right sides
(assuming that the system is written in canonical form, as (1) and (2)).
This condition, applied to the system (1),(2) has the form
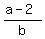 = = 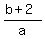 = 2.
So, you have these two equations (actually, the system of two equations) = 2.
So, you have these two equations (actually, the system of two equations)
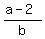 = 2, (3) = 2, (3)
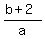 = 2 (4)
to determine two unknowns "a" and "b". Simplify this system:
a - 2 = 2b, (3')
b + 2 = 2a. (4')
You can solve it by using the substitution method.
Can you do it on your own? = 2 (4)
to determine two unknowns "a" and "b". Simplify this system:
a - 2 = 2b, (3')
b + 2 = 2a. (4')
You can solve it by using the substitution method.
Can you do it on your own?
For linear systems of two equations in two unknowns see the lessons
- Solution of a linear system of two equations in two unknowns by the Substitution method
- Solution of a linear system of two equations in two unknowns by the Elimination method
- Solution of a linear system of two equations in two unknowns using determinant
- Geometric interpretation of a linear system of two equations in two unknowns
- Solving word problems using linear systems of two equations in two unknowns
in this site.
|
|
|