Question 994285: The total profit $P, generated from the production and marketing of n items of a certain product is given by
P = −10800n − 4 n^3 + 600n^2 −122
How many items should be made for maximum profit? What is the maximum profit?
Enter your answers as a list [in square brackets] of the form: [ n, p]
for some number of items n and profit p
This is what I have
P = −10800n − 4 n^3 + 600n^2 −122
P' = -10800 -12n^2 + 1200n
-10800 -12n^2 + 1200n = 0
n = 10, n = 90
But I am not sure what to do from there?
Do I sub them in?
-10800 -12(10)^2 + 1200(10) = 0
-10800 -12(90)^2 + 1200(90) = 0
I'm lost!
Thank you!!
Answer by MathTherapy(10552)   (Show Source):
You can put this solution on YOUR website! The total profit $P, generated from the production and marketing of n items of a certain product is given by
P = −10800n − 4 n^3 + 600n^2 −122
How many items should be made for maximum profit? What is the maximum profit?
Enter your answers as a list [in square brackets] of the form: [ n, p]
for some number of items n and profit p
This is what I have
P = −10800n − 4 n^3 + 600n^2 −122
P' = -10800 -12n^2 + 1200n
-10800 -12n^2 + 1200n = 0
n = 10, n = 90
But I am not sure what to do from there?
Do I sub them in?
-10800 -12(10)^2 + 1200(10) = 0
-10800 -12(90)^2 + 1200(90) = 0
I'm lost!
Thank you!!
You're correct up to this point:  -------> 
Now, maximum profit (P) is realized at: 
With b being 1200, and a being - 12, becomes:  , or  , or 50
Number of units at which maximum profit occurs is: 
As mentioned before, this means that maximum profit is realized at n = 50 (I presume this should be in 000s, or millions) units
 -------- Substituting 50 for n
P, or maximum profit = - 30,000 + 60,000 - 10,800, or 
This results in: [n, P], or [   ]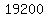
|
|
|
