Question 993749: Find point P(x,y) on line y=2x-1 so that its distance from point Q(4,3) is 2
Answer by Theo(13342)   (Show Source): (Show Source):
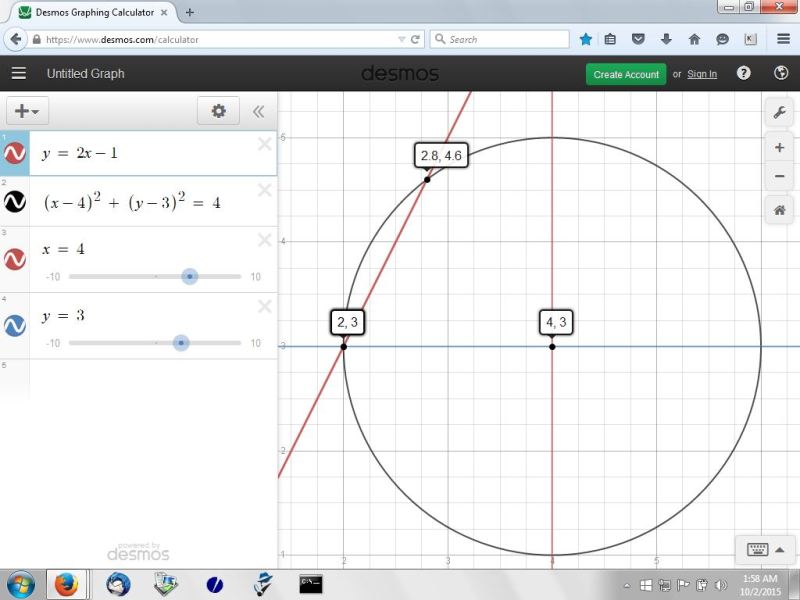
You can put this solution on YOUR website! you can solve this graphically easy enough if you have good graphing software.
using one, i found that two points satisfy the requirements.
those points are (2,3) and (2.8,4.60)
what you are looking for on the graph is the intersection of the line y = 2x-1 with the intersection of the circle whose equation is (x-4)^2 + (y-3)^2 = 4.
without graphing software it's not quite as easy, but can be done.
you are still looking for the intersection of the graph of the equations shown above, but you have to do it algebraically.
you have 2 equations:
y = 2x - 1
(x-4)^2 + (y-3)^2 = 4
the equation of y = 2x - 1 is a straight line.
the equation of (x-4)^2 + (y-3)^2 = 4 is a circle whose center is (4,3) and whose radius is 2.
replace y in the second equation with the value of y from the first equation to get:
(x-4)^2 + (2x-1-3)^2 = 4
simplify to get:
(x-4)^2 + (2x-4)^2 = 4
simplify the equation to get:
x^2 - 8x + 16 + 4x^2 - 16x + 16 = 4
combine like terms to get:
5x^2 - 24x + 32 = 4
subtract 4 from both sides of the equation to get:
5x^2 - 24x + 28 = 0
use the quadratic formula to find the values of x that satisfy that equation.
you will find that the values of x = 2 and x = 2.8 satisfy both equations and are therefore intersections of both equations on the graph.
when x = 2, y = 2x-1 becomes y = 3.
when x = 2.8, y = 2x-1 becomes 4.6.
the points on the circle that are also on the line are therefore (2,3) and (2.8,4.6)
both these points should be 2 units away from the center of the circle because the line segments formed by each of these points and the center of the circle is a radius of the circle.
the distance between two points on the graph is given by the equation:
d = sqrt((x1-x2)^2 + (y1-y2)^2).
the distance between (2,3) and (4,3) is equal to sqrt((4-2)^2 + (3-3)^2) which is equal to sqrt(2^2) which is equal to sqrt(4) which is equal to 2.
the distance between (2.8,4.6) and (4,3) is equal to sqrt((4-2.8)^2 + (3-4.6)^2) which is equal to sqrt(1.2)^2 + (-1.6)^2) which is equal to sqrt(1.44 + 2.56) which is equal to sqrt(4) which is equal to 2.
either one of these points will satisfy the requirements of this problem.
the graph of the line and the circle are shown below:
|
|
|