Question 988918: Consider the function f(x) = 1/x
I cannot use derivatives, my teacher requires using limits or other methods to solve.
(a). Find the slope of the L tangent to the graph of (3,f(3))
(b). Find an equation of the line L
(c). Find the x-intercept and y-intercept of L
Please explain how these are figured out. Very confused.
Also, what exactly is 3,f(3) are these just arb pts?
Thank you
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! The point (3,f(3)) is the same as (3,1/3) since f(3) = 1/3
Plug x = 3 into f(x) = 1/x to get f(3) = 1/3
===============================================================
===============================================================
Part a)


-------------------------------------------------------
Let's simplify the difference quotient
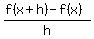
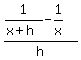
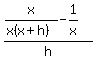
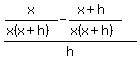



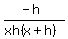
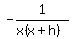
-------------------------------------------------------
Now apply the limit.
As h approaches 0, 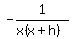 will approach will approach 
So the derivative function is 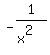
-------------------------------------------------------
Plug x = 3 into the derivative function to get 
Therefore, the slope of line L is 
===============================================================
===============================================================
Part b)
The slope of line L is 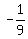 (found earlier). The tangent line L goes through (3,1/3) so x = 3 and y = 1/3. (found earlier). The tangent line L goes through (3,1/3) so x = 3 and y = 1/3.
Plug in  , ,  and and  into into  . Then solve for b. . Then solve for b.








The equation of the tangent line L is 
===============================================================
===============================================================
Part c)
The y-intercept is 2/3 or the point (0,2/3). This was found in part b) above.
The x-intercept is found by plugging in y = 0 and solving for x







The x-intercept is 6, which is the same as the point (6,0)
===============================================================
===============================================================
Graph
 is in green is in green
 is in blue (tangent line at (3,1/3)) is in blue (tangent line at (3,1/3))
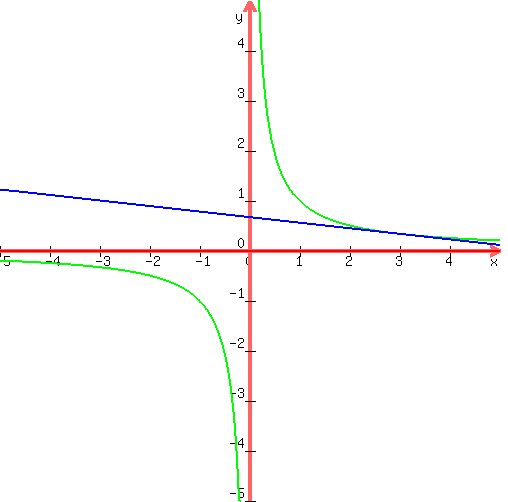
-------------------------------------------------------
If you need more help, or if you have any questions about the problem, feel free to email me at
jim_thompson5910@hotmail.com
|
|
|