Question 987872: Let  and and 
Find and simplify the quotient:
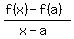 = =
Then find the slope 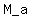 of the line tangent to the graph of f at the point (a,f(a)) of the line tangent to the graph of f at the point (a,f(a))
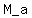 = =
Please give details on how this is solved very confused.
Thank you
Found 2 solutions by Edwin McCravy, solver91311:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
First of all, if you use triple brackets improperly,
it messes everything up. So don't use them next time
if you you don't understand the triple bracket notation
program used on this site I rewrote your problem
correctly in the triple bracket program.
Let  and and  Find and simplify the quotient:
Find and simplify the quotient:
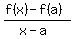 Then find the slope
Then find the slope  of the line tangent to the graph
of f at the point (a,f(a)) of the line tangent to the graph
of f at the point (a,f(a))
 ---------------------
Since they tell you that a=3, rewrite the problem using 3 for a
and it will make more sense:
Find and simplify the quotient:
---------------------
Since they tell you that a=3, rewrite the problem using 3 for a
and it will make more sense:
Find and simplify the quotient:
 Then find the slope
Then find the slope 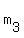 of the line tangent to the graph
of f at the point (3,f(3)) of the line tangent to the graph
of f at the point (3,f(3))
 ------------------------------
Now since you know what f(x) is, you can find f(3),
------------------------------
Now since you know what f(x) is, you can find f(3),
 So now rewrite the problem with 38 for f(3)
--------------------------------
Find and simplify the quotient:
So now rewrite the problem with 38 for f(3)
--------------------------------
Find and simplify the quotient:
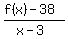 Then find the slope
Then find the slope 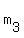 of the line tangent to the graph
of f at the point (3,38) of the line tangent to the graph
of f at the point (3,38)
 --------------------------------
We are trying to find the slope of a line tangent to the graph of
--------------------------------
We are trying to find the slope of a line tangent to the graph of
 at the point (3,38)
The slope formula at the point (3,38)
The slope formula  when applied to the
two points when applied to the
two points 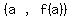 , which is (3,38) and , which is (3,38) and 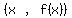 gives gives
 This is the slope of the line that goes through the two points
(3,38) and the variable point
This is the slope of the line that goes through the two points
(3,38) and the variable point 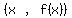 As the variable point
As the variable point 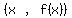 gets closer and
closer to the fixed point gets closer and
closer to the fixed point 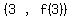 which is the
point (3,38), the line through them gets closer and closer to being
a tangent line. We would like to make x equal to 3, for that would
cause the line to become tangent but we can't yet.
We cannot yet choose x=3 in the slope formula which is the
point (3,38), the line through them gets closer and closer to being
a tangent line. We would like to make x equal to 3, for that would
cause the line to become tangent but we can't yet.
We cannot yet choose x=3 in the slope formula
 because we get:
because we get:
 which gives 0 in the denominator.
So you see we cannot substitute x=3 yet, because the
denominator will be zero.
Next we substitute
which gives 0 in the denominator.
So you see we cannot substitute x=3 yet, because the
denominator will be zero.
Next we substitute 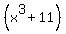 for for  and and
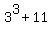 for for 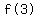 in in

 and simplify:
and simplify:

 Factor the numerator as the difference of two cubes:
Factor the numerator as the difference of two cubes:
 Now we can cancel the (x-3)'s leaving
Now we can cancel the (x-3)'s leaving
 Now we CAN let x=3 because we no longer have a
denominator to be 0.
So when we substitute x=3 we get
Now we CAN let x=3 because we no longer have a
denominator to be 0.
So when we substitute x=3 we get

 That's the slope of a line tangent to the graph of
That's the slope of a line tangent to the graph of
 at the point (3,38)
So that slope at the point (3,38)
So that slope  Edwin
Edwin
Answer by solver91311(24713)   (Show Source): (Show Source):
|
|
|