Question 984771: if x = y+z, y = z+x, z = x+y, then what is the value of (1/(x+1)) + (1/(y+1)) + (1/(z+1))?
How to solve this?
Answer by ikleyn(52784)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If x = y+z, y = z+x, z = x+y, then what is the value of 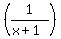 + +  + + 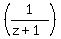 ? ?
-------------------------------------------------------------------------------------------------
You have the system of three linear equations with three unknowns
 . .
Add all three equations. You will get
-x - y - z = 0, or
x + y + z = 0. (*)
Now, add the last equation and the first one of the system. You will get
2x = 0, and, hence, x = 0.
Next, add the equation (*) and the second equation of the system. You will get
2y = 0, and, hence, y = 0.
Finally, add the equation (*) and the third equation of the system. You will get
2z = 0, and, hence, z = 0.
Thus your system has a unique solution x = y = z = 0.
Hence, the expression under the question is
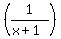 + +  + + 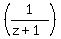 = 3. = 3.
|
|
|