SOLUTION: Hello! What are all the rational zeros of the function? f(x) = 2x^4 – 13x^3 + 12x^2 + 52x – 80 Thank you!

It's in descending order, so look at the numbers on both ends,
the 80 on the far right and the 2 on the far left.  Ignore signs
for now. 

All the factors of 80 are 1,2,4,5,8,10,16,20,40,80.

All the factors of 2 are 1 and 2.

Make all possible fractions with a numerator as a factor of 80 and
a denominator as a factor of 2.  Some of the fractions will reduce
and become duplicates.

,,,,,,,,,,,,,,,,,,,

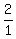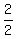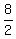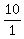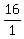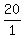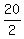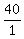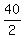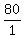Then we reduce the ones that will reduce and toss out the duplicates:

,,,,,,,,,,,,

Finally we put a  before every one because they could be either positive or
negative.

,,,,,,,,,,,,

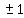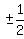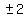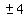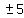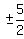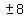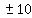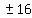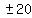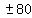Now we have to use trial and error to find one of those, if there are any, that
will prove to be a rational zero.  We try 1, the easiest one:

1 | 2 -13  12 52 -80
  |     2 -11  1  53 
    2 -11   1 53 -27

So 1 is not a zero, because we get -27 remainder instead of 0


So we try the next easiest one, 2

2 | 2 -13  12  52 -80
  |     4 -18 -12  80 
    2  -9  -6  40   0

So 2 is a zero, and now we have factored f(x) as

f(x) = (x-2)(2x³-9x²-6x+40) 

Now we try the next easiest one, -1.  But we don't try it in the original
polynomial.  Instead we try it in the cubic factor 2x³-9x²-6x+40 that we
got from the synthetic division.


-1 | 2  -9  -6  40
   |    -2  11  -5   
     2 -11   5  35

So -1 is not a zero,


Now we try the next easiest one, -2

-2 | 2  -9  -6  40
   |    -4  26 -40   
     2 -13  20   0

So -2 is a zero, and now we have factored f(x) as

f(x) = (x-2)(x+2)(2x²-13x+20) 

We can now use regular factor methods to factor 2x²-13x+20
as (x-4)(x-5), and now we have factored the polynomial 
completely:

f(x) = (x-2)(x+2)(x-4)(2x-5)

The zeros all rational are found by setting each = 0 and solving.


x-2=0;  x+2=0;  x-4=0;  2x-5=0
  x=2;    x=-2;   x=4     2x=5
                           x=

Rational zeros: 2, -2, 4, and 5/2

Edwin