Question 976765: For the following systems of equations in echelon form, tell how many solutions there are in nonnegative integers. x - 7y+4z = 75; 2y+7z=60.
Thanks a bunch!
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! our matrix

Find the pivot in the 1st column in the 1st row

Make the pivot in the 2nd column by dividing the 2nd row by 2
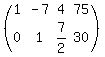
Eliminate the 2nd column
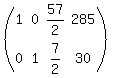
Solution set:


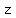 - free - free
Therefore the solutions can be written as
( , ,  , ,  ) = ( ) = (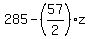 , ,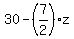 , , ) )
Because we want to find non-negative solutions, we have three inequalities



so,






and

so, the integer values of  satisfying all of those inequalities satisfying all of those inequalities  , , , and , and  are are
 = = , , , , , , , , , , , , , , , ,
so, there will be nine non-negative solutions
|
|
|