SOLUTION: If (x-a)(x-b)=1 and a-b+5=0 Then [(x-a)^3-1]/(x-a)^3 = ? (X-a) power of 3 -1/(x-a) power of 3=

 If (x-a)(x-b)=1 and a-b+5=0
Then
(x-a)^3-1/(x-a)^3 = ?

71 +- 13V29

Let x-a = u.  Then x = a+u

Making those substitutions the problem becomes:

If u(a+u-b)=1 and a-b+5=0

Then
u^3-1/u^3 = ?

Since a-b+5=0, then a = b-5

Substitute in

u(a+u-b)=1

u(b-5+u-b) = 1

u(-5+u) = 1

-5u+u² = 1

u²-5u-1 = 0

To avoid a conflict of letters, we use capital letters 
in the quadratic formula










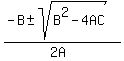
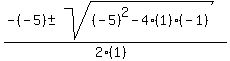
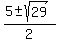We want to find : 

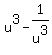We factor as the difference of two cubes:

(1)  

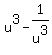
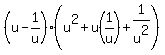
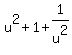We need u2, , , 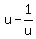and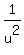  



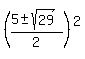Let's first use the + sign, 











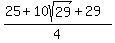
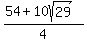
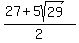
Rationalizing the denominator:







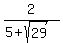
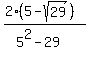
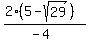
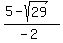
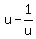
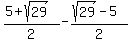
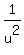
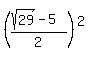
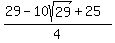
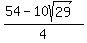
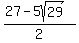Going back to equation (1)







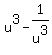
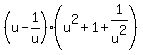
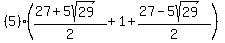
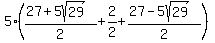
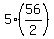
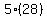
If we do the same with ,
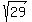all the signs of the terms in  will reverse their signs,
and we'll still get 140.

Answer: 140

Edwin