Question 971541: Solve on the interval [0, 2pi]
2cos*2x=1
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! we'll do this in degrees and then translate to radians.
it's easier to show.
cos(2x) = .5
find cos^-1(.5) and you get 2x = 60 degrees.
that means that x is equal to 30 degrees.
the period of x is equal to 180 degrees because the frequency of x is equal to 2.
within that period of 180 degrees, you have 4 quadrants.
cosine is positive in the first and fourth quadrant.
30 degrees is in the first quadrant.
180 - 30 = 150 degrees is in the fourth quadrant.
within a 360 degree interval, you will get two full cycles of cosine(2x).
the cosine will be .5 at 30, 150, 30 + 180, 150 + 180.
that equates to 30, 150, 210, 330 degrees.
i'll show you the graph in degrees and then translate to radians.
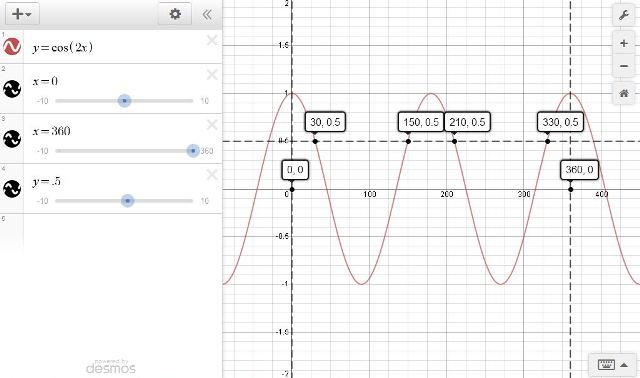
here's the same graph in radians.
look under the graph for further comments.
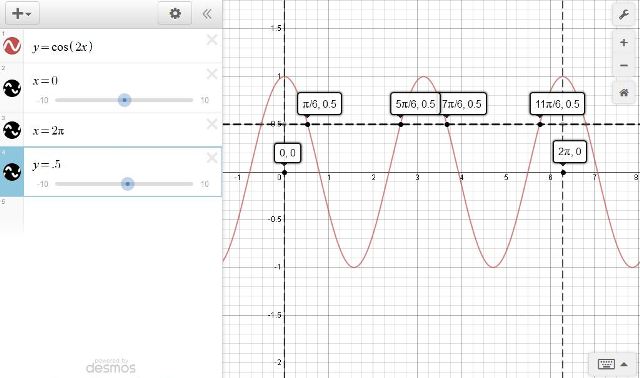
instead of an interval from 0 to 360, you have an interval from 0 to 2pi.
conversion factor from degress to radians is radians = degrees * pi / 180.
30 degrees would be equal to 30/180 * pi which is equal to pi/6.
150 degrees would be equal to 150/180 * pi which is equal to 5pi/6.
210 degrees would be equal to 210/180 * pi which is equal to 7pi/6.
330 degrees would be equal to 330/180 * pi which is equal to 11pi/6.
|
|
|