Find the equation for the parabola...
Its equation is
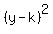

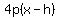 if it opens up or down,
with directrix y=k-p and focus (0,k+p)
if p is positive it opens up, if p is negative it opens down.
or
{{(x-h)^2}}}
if it opens up or down,
with directrix y=k-p and focus (0,k+p)
if p is positive it opens up, if p is negative it opens down.
or
{{(x-h)^2}}}
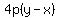 if it opens right or left.
with directrix x=h-p and focal point (h+p,0)
if p is positive it opens right, if negative it opens left.
if it opens right or left.
with directrix x=h-p and focal point (h+p,0)
if p is positive it opens right, if negative it opens left.
...that has its vertex at the origin
So h=0 and k=0
Its equation is


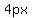 if it opens up or down,
with directrix y=-p and focus (0,p)
if p is positive it opens up, if p is negative it opens down.
or
{{x^2}}}
if it opens up or down,
with directrix y=-p and focus (0,p)
if p is positive it opens up, if p is negative it opens down.
or
{{x^2}}}
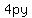 if it opens right or left.
with directrix x=-p and focal point (p,0)
if p is positive it opens right, if negative it opens left.
if it opens right or left.
with directrix x=-p and focal point (p,0)
if p is positive it opens right, if negative it opens left.
...and the focal point is 296 units above the directrix.
So it opens upward. The vertex is exactly half-way between the focal point
and the directrix line. The focal point is half of 296 or 148 units above
the vertex. The focal point is (0,148) and the directrix's equation is
y = -148, and p=+148
So its equation is


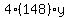


 or
or 

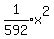
 Edwin
Edwin