Question 969578: x^2-2x+sqrt(x^2-2x-2)=4
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
You need to isolate the irrational expression.

Square both sides.


 -----You could take the rest of the process. You want to try looking for Rational Roots to try to factorize the polynomial. (Rational Roots Theorem). Several possible roots to test for: -----You could take the rest of the process. You want to try looking for Rational Roots to try to factorize the polynomial. (Rational Roots Theorem). Several possible roots to test for:
The plusses and minuses of 1,2,3,6,9; and there might be complex roots - not know until you try.
Roots Found Through Synthetic Division:
-1, 3,
Resulting coefficients after that give 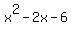 discriminant of 28, so two more IRRATIONAL roots. General solution to quadratic equation will give -1-sqrt(7) and -1+sqrt(7). discriminant of 28, so two more IRRATIONAL roots. General solution to quadratic equation will give -1-sqrt(7) and -1+sqrt(7).
----------------------------------------------------
Solution Set:
-1, 3, 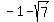 , and , and 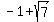 . .
-----------------------------------------------------
|
|
|