Question 969538: 1-sinx/cosx=cosx/1+sinx
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! NOTE:
I believe you meant  . .
If that was not what you meant, then I solved the wrong problem.
You could write  as as
(1-sinx)/cosx=cosx/(1+sinx) , because
1-sin(x)/cos(x)= and cos(x)/1+sin(x)= and cos(x)/1+sin(x)=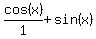 . .
The parentheses are implicit in  . .
The long horizontal line between numerator and denominator is a powerful grouping symbol that indicates that numerator and denominator must be calculated before doing the division.
When you cannot write two lines (as when you are entering calculations into a calculator or spreadsheet) you need to write the implicit parentheses.
The expressions in  do not exist (are undefined) when the denominators are zero. do not exist (are undefined) when the denominators are zero.
 happens for happens for  , ,  , and all co-terminal angles. , and all co-terminal angles.
In general, we could say that  for every integer for every integer 
makes  and cannot be a solution to the equation above. and cannot be a solution to the equation above.
The values of  that make that make  <---> <---> are are
 and all co-terminal angles. and all co-terminal angles.
Those values will be excluded if we exclude  for every integer for every integer 
to make 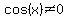 . .
As long as 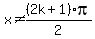 for every integer for every integer  , ,
which makes 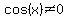 and and 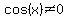 , we can multiply both sides of , we can multiply both sides of
 times times 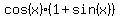
to get the equivalent equations
 ---> ---> ---> ---> , ,
and since the last equation is a trigonometric identity,
true for all values of  , ,
the solution to  is all values of is all values of  , ,
and the solution to 
is all values of  such that such that 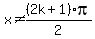 for every integer for every integer  . .
|
|
|