 Before using elimination, get rid of the fractions by
multiplying them through by the least common denominator of 4:
Before using elimination, get rid of the fractions by
multiplying them through by the least common denominator of 4:

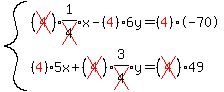
 We notice that the y terms will cancel if we multiply the second
equation through by 8 to make the +3y become +24y. then it will
cancel with the -24y term in the first equation:
We notice that the y terms will cancel if we multiply the second
equation through by 8 to make the +3y become +24y. then it will
cancel with the -24y term in the first equation:
 ------------------------------
------------------------------



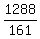


 Finish by subtituting 8 for x in any of the above equations
which contain both letters. I'll pick this one
Finish by subtituting 8 for x in any of the above equations
which contain both letters. I'll pick this one




 The solution is (x,y) = (8,12)
--------------------------------------
b.)
The solution is (x,y) = (8,12)
--------------------------------------
b.)  Multiply the first one through by 4
Multiply the first one through by 4

 Now we need to line the terms up su that the x terms come first,
the y-terms come second, the equal signs come third and the constant
terms come fourth. We do that by adding and subtracting terms from
both sides until they get like this:
Now we need to line the terms up su that the x terms come first,
the y-terms come second, the equal signs come third and the constant
terms come fourth. We do that by adding and subtracting terms from
both sides until they get like this:
 We notice that the x terms will cancel if we multiply the first
equation through by -2 to make the x become -2x. Then it will
cancel with the 2x term in the second equation:
We notice that the x terms will cancel if we multiply the first
equation through by -2 to make the x become -2x. Then it will
cancel with the 2x term in the second equation:
 ------------------------------
------------------------------



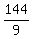


 Finish by subtituting 16 for y in any of the above equations
which contain both letters. I'll pick this one
Finish by subtituting 16 for y in any of the above equations
which contain both letters. I'll pick this one




 The solution is (x,y) = (-2,16)
Edwin
The solution is (x,y) = (-2,16)
Edwin