Question 956614: solving set of linear by guasian elimination method,a+2b+3c=5,3a-b+2c=8,4a-6b-4c=-2 find a,b and c
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your solution is:
a = -1
b = -3
c = 4
replace a with -1 and b with -3 and c with 4 in all three of your equations and they should all hold true.
when you do that:
a + 2b + 3c = 5 becomes -1 - 6 + 12 = 5 which becomes -7 + 12 = 5 which becomes 5 = 5.
3a - b + 2c = 8 becomes -3 + 3 + 8 = 8 which becomes 8 = 8.
4a - 6b - 4c = -2 becomes -4 + 18 - 16 = -2 which becomes -20 + 18 = -2 which becomes -2 = -2.
the solution is good.
there's a nice little tool on the web that you can use to check your work.
that tool can be found here:
http://www.gregthatcher.com/Mathematics/GaussJordan.aspx
the tool may not solve it exactly as you would solve it manually, but you should get the same answer that the tool gives you.
i only recommend you use the tool to check your work because you need to do it manually to really appreciate the process and to prepare you for taking your test.
the gauss method works from tableaus.
each tableau is the matrix taken one step further to solution by using row manipulation methods.
the tool uses the gauss-jordan method which is the gauss method taken one step further.
my manual calculations are shown below:
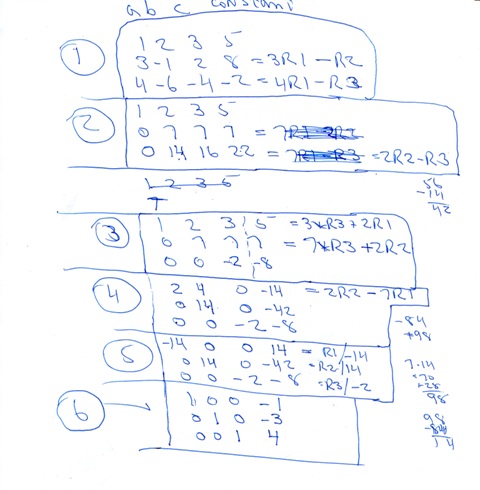
in my manual calculations, the gauss method would take you to step 3.
with that tableau, it's an easy matter to solve first for c, then solve for b, then solve for a.
the third row allows you to solve for c.
the second row allows you to solve for b.
the first row allows you to solve for a.
in my manual calculations, the gauss-jordan method would take you to step 6.
the gauss-jordan method takes you all the way until you are left with the tableau shown in step 6.
in that tableau, you can automatically see that:
c = 4
b = -3
a = -1
since you were interested in gauss and not gauss-jordan, than step 3 is where you would want to stop.
from step 3 output, you would solve for c from row 3 as follows:
-2c = -8
divide both sides of the equation by -2 to get:
c = 4
once you have c = 4, you would then solve for b from row 2 as follows:
7b + 7c = 7
replace c with 4 to get:
7b + 28 = 7
subtract 28 from both sides to get:
7b = -21
divide both sides by 7 to get:
b = -3
once you have b = -3 and c = 4, you would then solve for a from row 1 as follows:
a + 2b + 3c = 5
replace c with 4 and b with -3 to get:
a + 2*-3 + 3*4 = 5 which becomes:
a - 6 + 12 = 5 which becomes:
a + 6 = 5 which becomes:
a = -1
you get a = -1, b = -3, c = 4
this is the same solution that gauss-jordan gave you in step 6.
gauss method and gauss-jordan method work by what is called row manipulation.
the matrix or array is created from the coefficients of the variables and from the constant term.
it's called an augmented matrix.
the variables are on the left side of the equation and the constant term is on the right side of the equation.
the last column of the matrix is the constant term that is on the right side of the equation.
here's a reference that talks about gauss method and gauss-jordan method.
it's as good as any, maybe even a little clearer than some.
http://www.cliffsnotes.com/math/algebra/linear-algebra/linear-systems/gaussian-elimination
|
|
|