SOLUTION: Given the equation x^2 - 12x + y^2 - 16y + 84=0, complete the square for both x and y. What is the result? How do I do this?

Algebra ->  Equations -> SOLUTION: Given the equation x^2 - 12x + y^2 - 16y + 84=0, complete the square for both x and y. What is the result? How do I do this?       Log On


   

Question 932792: Given the equation x^2 - 12x + y^2 - 16y + 84=0, complete the square for both x and y. What is the result? How do I do this?
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
x%5E2+-+12x+%2B+y%5E2+-+16y+%2B+84=0
%28x%5E2+-+12x%2B__%29+%2B+%28y%5E2+-+16y+%2B__%29%2B+84=0
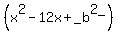since we need b%5E2 to have a%5E2%2B2ab%2Bb%5E2 and we are given %28x%5E2+-+12x%2B_b%5E2_%29 , where a=1, 2ab=12,then =>2%2A1%2Ab=12=>b=6 and b%5E2=36
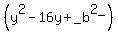and %28y%5E2+-+16y+%2B_b%5E2_%29, a=1, 2ab=-16,then =>2%2A1%2Ab=-16=>b=-8 and b%5E2=64
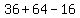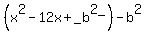so, to complete the square, first write 84 as 36%2B64-16}, add 36 to %28x%5E2+-+12x%2B_b%5E2_%29+-b%5E2 and subtract it so the equation doesn't change
%28x%5E2+-+12x%2B36%29+-36%2B+%28y%5E2+-+16y+%2B64%29-64%2B+84=0
%28x%5E2+-+6%29%5E2+%2B+%28y%5E2+-8%29%5E2-36-64%2B+84=0
%28x%5E2+-+6%29%5E2+%2B+%28y%5E2+-8%29%5E2-100%2B+84=0
%28x%5E2-6%29%5E2%2B%28y%5E2-8%29%5E2-16+=+0
%28x%5E2-6%29%5E2%2B%28y%5E2-8%29%5E2=16+
so, you have a circle with center at (6,-8) and radius r=4