If 
is a factor of 
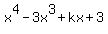, what is the value of k?
1. The remainder theorem tells us that you get the same thing when you
substitute 3 into a polynomial as you get when you divide the polynomial
by x-3 and take only the remainder.
2. The factor theorem thell us that since x-3 is a factor of the polynomial
then if we divided the polynomial by x-3, the remainder would be 0.
Putting these two facts together we can see that if we substituted 3 into
the polynomial, we will get the same result as the remainder would be if we
divided the polynomial by x-3. And furthermore due to 2, that remainder must
be 0. So all we have to do is substitute 3 for x in the polynomial and set
it equal to 0.
So substituting 3 for x in x^4-3x^3+kx+3 gives
3^4-3(3)^3+k(3)+3
81-3(27)+3k+3
81-81+3k+3
3k+3
Setting 3k+3 = 0
3k = -3
k = -1
Now let's check to see if we are right. If we are then the polynomial
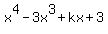becomes 
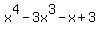. We will divide that
synthetically by x-3 to see if we get a 0 remainder. First we must
insert a +
term, and write it as 
.
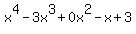3 | 1 -3 0 -1 3
| 3 0 0 -3
1 0 0 -1 0
Sure enough, we do get 0 for a remainder.
So k = -1 is correct.
Edwin
