Question 927517: Find all real values of b such that the equation: x^2 + bx + 6b = 0
only has integer roots.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find all real values of  such that the equation: such that the equation:
 only has integer roots. only has integer roots.
Theorem:
Let  , being a quadratic trinomial with integer coefficients , being a quadratic trinomial with integer coefficients  , ,  , ,  . Then, both roots or zeros of . Then, both roots or zeros of  are integers; if, and only if, are integers; if, and only if,
(i)
The integer  is an integer or perfect square. is an integer or perfect square.
and
(ii) The leading coefficient  is a divisor of both is a divisor of both  and and  . .
in your case, The leading coefficient  is a divisor of both is a divisor of both  and and  because because 
but, we need  ; so, ; so,
 if discriminant if discriminant  (Positive Discriminant ), we will have Two Real Solutions (Positive Discriminant ), we will have Two Real Solutions


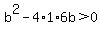 ........solve for ........solve for 
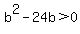
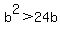
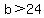
solution is 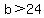
let have first one greater then : :
 ...only has integer roots ...only has integer roots
proof:





 and and  ->solutions are integer roots ->solutions are integer roots

|
|
|