SOLUTION: I am printing a sticker. The width of the sticker = 280cm The height of the sticker = 254cm The no. of meter² of the sticker = 2.8 X 2.54 = 7.112 meter² If 7.112 meter² at $55/

I am printing a sticker.
The width of the sticker = 280cm
The height of the sticker = 254cm
The no. of meter² of the sticker = 2.8 X 2.54 = 7.112 meter²
If 7.112 meter² at $55/meter² cost $391.16 to produce,
how much do I need to reduce the width and height of the sticker so that a
total cost of $245 will be charged to the client buying the sticker?
You need to keep the width vs height proportionate so that they are both
reduced proportionally.
:-)
Good luck!
Patrick A. 
PS I need a general formula please so that I can apply it to the rest of the
dimensions of stickers which I am producing, and for which I need to reduce
their cost.

Since you want a general formula, let's reword the problem with
unknown constants instead of known values, and, to make it easier,
keep all units in meters and meters²:

Rewording with unknown constants

I am printing a sticker.
The width of the sticker = W meters
The height of the sticker = H meters
The area of the sticker = W times H = WH meter² 
At $M/meter², the cost is $WHM to produce,
how much do I need to reduce the width and height of the sticker so 
that a total cost of $C will be charged to the client buying the 
sticker?

>>...The (old) width of the sticker = W...<<
>>...The (old) height of the sticker = H...<<

Let x = the number (which will be less than one) by which we must
multiply both the base and the height.

(The new width) = (The old width times x) = Wx
(The new height) = (The old height times x) = Hx
(The new area) = (The new width tmes the new height) = (Wx)(Hx) = WHx² meter². 

>>...$M/meter²...<< 

(Cost of new area) = (New area times $M) = (WHx²)(M) = WHMx²

We want (Cost of new area) to equal $C, so we set

WHMx² = C

Divide both sides by WHM

 = 

 = 

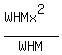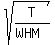
Take square root of both sides:

 = 

That's the general formula for the number to multiply
both the width W and the height H by to reduce the cost from
$WHM to $C, where $M is the price per square meter.

However, we must answer the question:

>>...how much do I need to reduce the width and height of the sticker...<< 

We must reduce the width from W meters to xW meters, so that means we must
reduce the width by (W - xW) meters or by W(1-x) meters.

We must reduce the heigth from H meters to xH meters, so that means we must
reduce the height by (H - xH) meters or by H(1-x) meters.

So for this problem, we substitute W = 280cm = 2.8m, H = 254cm = 2.54m,
M = $55, C = $245

 = 

 = 

 = .7914178174

We must reduce the width from W meters to xW meters, so we must reduce
the width by (W - xW) meters or by W(1-x) meters.

We must reduce the width from 2.8 meters to (.7914178174)2.8 or 
2.215969889 meters, so we must reduce the width by (2.8 - 2.215969889) 
meters or by .584030111 meters, or about 58.4 centimeters. 

We must reduce the height from H meters to xH meters, so we must reduce
the height by (H - xH) meters or by H(1-x) meters.

We must reduce the height from 2.54 meters to (.7914178174)2.54 or
2.010201256 meters, so we must reduce the height by (2.54 - 2.010201256) 
meters or by .5297987437 meters, or about 53.0 centimeters.

Edwin