SOLUTION: What is the equation of line that is perpendicular to 96x-24y-72=0 and passing through the midpoint between (-22,6) and (14,-16)? Kindly help !!

Algebra ->  Equations -> SOLUTION: What is the equation of line that is perpendicular to 96x-24y-72=0 and passing through the midpoint between (-22,6) and (14,-16)? Kindly help !!      Log On


   

Question 902096: What is the equation of line that is perpendicular to 96x-24y-72=0 and passing through the midpoint between (-22,6) and (14,-16)?
Kindly help !!
Found 2 solutions by josgarithmetic, Edwin McCravy:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Simplify your given equation!
96x%2F6-24y%2F6-72%2F6=0
16x-4y-12=0
highlight_green%284x-y-3=0%29

4x-y-3=0 can be solved for y.
highlight_green%28y=4x-3%29
Which is slope-intercept form for your given, now simplified, equation.

The line perpendicular to the given line will have slope -%281%2F4%29, which is the negative
reciprocal of 4. That is how perpendicular lines in a plane work. The line you are looking
for is y=-x%2F4%2Bb and you do not yet know what is b.

Next, you want to know the midpoint of the two given points, because you are told that
y=-x%2F4%2Bb must include this point.
MIDPOINT: x=%28-22%2B14%29%2F2=-4; y=%286%2B%28-16%29%29%2F2=-5
This midpoint is (-4,-5).

You can solve the equation you want for b and use this found point (-4,-5) to get the value
of b.
b=y-mx
b=y-%28-1%2F4%29x
b=-5-%28-1%2F4%29%28-4%29
b=-5-1
highlight_green%28b=-6%29

Finish writing the equation asked for.
highlight%28y=-x%2F4-6%29

Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
What is the equation of line that is perpendicular to 96x-24y-72=0 and passing through the midpoint between (-22,6) and (14,-16)
First we find the slope of the line whose equation is

     96x-24y-72=0

by solving it for y to get it in the form y=mx+b

           -24y=-96x%2B72

Divide ever term through by -24

              y=4x-3
              
Compare that to y=mx+b and we see that m=4 and b=-3. We only need
the slope 4.  We don't need the y-intercept.

Any line perpendicular to a line whose slope is 4, has a slope which
is the reciprocal of 4 with the sign changed.  Therefore the slope
of the desired line will have slope -1%2F4.

Now we use the midpoint formula to find the midpoint between (-22,6) and
(14,-16)


Midpoint = 

where (x1,y1) = (-22,6)
and where (x2,y2) = (14,-16)

Midpoint = 

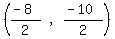Midpoint = %28matrix%281%2C3%2C%28-8%29%2F2%2C+%22%2C%22%2C%28-10%29%2F2%29%29

Midpoint = (-4,-5)

Next we use the point slope formula:


y - y1 = m(x - x1)
where m=-1%2F4 and (x1,y1) = (-4,-5)

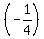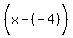y - (-5) = %28-1%2F4%29%28x%5B%22%22%5D-%28-4%29%29

y + 5 = -1%2F4(x + 4)

y + 5 = -1%2F4x - 1

    y = -1%2F4x + 6

Edwin