SOLUTION: Respected sir, Factorize x^4-1 I have solved it like this: (x^2)2-(1)^2 (Formula a^2-b^2= (a+b)(a-b) (x^2+1)(X^2-1) But the answer is (x^2+1)(x+1)(x-1) Sir, my point

Algebra ->  Equations -> SOLUTION: Respected sir, Factorize x^4-1 I have solved it like this: (x^2)2-(1)^2 (Formula a^2-b^2= (a+b)(a-b) (x^2+1)(X^2-1) But the answer is (x^2+1)(x+1)(x-1) Sir, my point      Log On


   

Question 8891: Respected sir,
Factorize x^4-1
I have solved it like this:
(x^2)2-(1)^2 (Formula a^2-b^2= (a+b)(a-b)
(x^2+1)(X^2-1)
But the answer is (x^2+1)(x+1)(x-1)
Sir, my point is if the 2nd term i.e. (x^2-1)is further factorized to (x+1) (x-1), then why not the first term i.e. (x^2+1). Pl. make me understand.

Answer by mrduffner(11) About Me  (Show Source):
You can put this solution on YOUR website!
You don't know how glad I am that you asked this question. This is a common factoring problem you will see in algebra books. Lets run through it from the beginning.
x%5E4-1
This expression is a difference of squares. The description of a difference of squares is an expression in which there are two terms, both being perfect squares and the sign of the second term being negative. I see you understand how to factor a difference of squares.
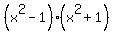
%28x%5E2-1%29%28x%5E2%2B1%29
In our answer, we have another difference of squares. Since the problem most likely said to factor completely, we cannot leave it. So we factor again.
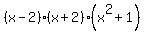
%28x-2%29%28x%2B2%29%28x%5E2%2B1%29
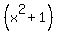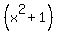Now, we have fully factored the problem. The reason you do not factor the %28x%5E2%2B1%29 is because it is not a difference of squares. The reason that a difference of squares can be factored and this expression can't is in the alternating signs in the factoring of a difference of squares. When you factor, one of your factors has a minus sign, and the other has a plus sign. To factor %28x%5E2%2B1%29, we would need two numbers that when multiplied, produced a +1. We have two choices, -1 and -1 or +1 and +1. But when we FOIL (FIRST, OUTER, INNER, LAST), when we multiply the outer and inner we would either get -2x or 2x. 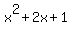Therefore, the expression would have to be either x%5E2-2x%2B1 or x%5E2%2B2x%2B1. Like I said, it really is all in those alternating signs. It is the alternating signs that makes the second term negative in the difference of squares, and it is the alternating signs that makes the Outer and the Inner terms negative opposites so that they cancel. I hope this helps.